4.3.2空间两点间的距离公式-(3)VIP免费

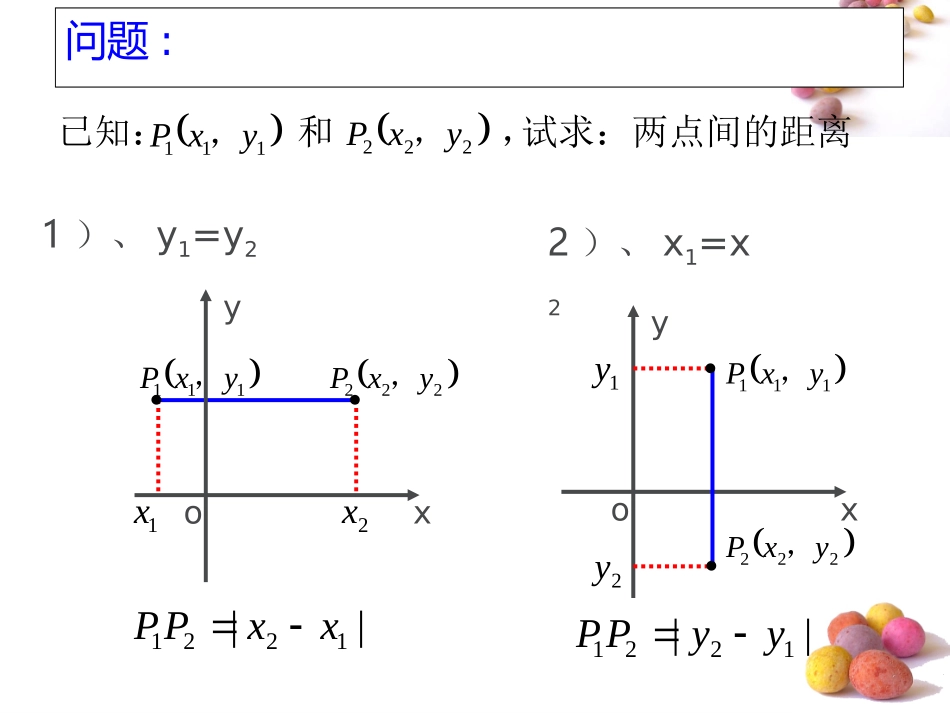
3.3.2两点间的距离问题引入：已知点A（-1，3），O（0，0），B（3，-1）C（2，2），试问：四边形AOBC是什么四边形？如果把问题一般化就有如下问题：答：AO//BC,OB//AC,四边形AOBC是平行四边形。xoyABC是菱形四边形又AOBCOCAB或AO=AC，得四边形AOBC是菱形AO的长怎样求？AC的长怎样求？问题:试求：两点间的距离已知：和，111yxP，222yxP，xoy1）、y1=y21x2x2）、x1=x2xoy1y2y||1221xxPP||1221yyPP111yxP，222yxP，111yxP，222yxP，构建数学:xoy21yxQ，2121,)3yyxx、21221221)()(yyxxPP两点间的距离111yxP，222yxP，111yxP，222yxP，问题引入：已知点A（-1，3），O（0，0），B（3，-1）C（2，2），试问：四边形AOBC是什么四边形？xoyABCAO=AC，得四边形AOBC是菱形AO的长怎样求？AC的长怎样求？答：AO//BC,OB//AC,四边形AOBC是平行四边形。例题分析例题分析.|||,|||,),7,2(),2,1(1的值并求得使轴上求一点在已知点例PAPBPAPxBA解：设所求点为P(x,0)，于是有114xx)7(02)(x|PB|52xx2)(01)(x|PA|222222114xx52xx得|PB||PA|由22解得x=1，所以所求点P(1,0)22222)(01)(1|PA|例2.证明平行四边形四条边的平方和和等于两条对角线的平方和。证明：以A为原点，AB为x轴建立直角坐标系。xyABCD(0,0)(a,0)(b,c)(a+b,c)则四个顶点坐标分别为A(0,0),B(a,0),D(b,c)C(a+b,c)22||CDa222||ADbc222||BCbc222||()BDbac2222222||||||||2()ABCDADBCabc22222||||2()ACBDabc222222||||||||||||ABCDADBCACBD因此，平行四边形四条边的平方和等于两条对角线的平方和。解析法第二步:进行有关代数运算第三步:把代数运算结果翻译成几何关系。第一步:建立坐标系，用坐标表示有关的量。练习1:用坐标法解决一些几何问题求证:直角三角形斜边上的中线等于斜边的一半.已知:Rt△ABC中，D是斜边BC上的中点.求证:AD=.BC21yxAC(0,0)(a,0)(0,b)BD,22ab2.已知:△ABC中，D是BC边上的中点.求证:)(22222BDADACABACBDyx练习2:应用—判定△的形状练习3:两点距离公式逆应用1、平面内两点P1(x1,y1),2(x2,y2的距离公式是小结小结2、坐标法证明简单平面几何问题的步骤第一步：建立坐标系，用坐标表示有关的量；第二步：进行有关的代数运算；第三步：把代数运算结果“翻译”所几何关系.21221221)()(yyxxPP111yxP，222yxP，例1:已知的顶点坐标为A（-1，5），B（-2，-1），C（4，7），（1）求BC边的长；（2）求BC边上的中线AM的长；（3）求BC边上的中线AM所在直线的方程。ABC一般地，三角形的顶点为A（x1，y1），B（x2，y2），C（x3，y3）,三角形的重心是M（x0，y0），则：3332103210yyyyxxxx