1.1.2弧度制和弧度制与角度制的换算VIP免费

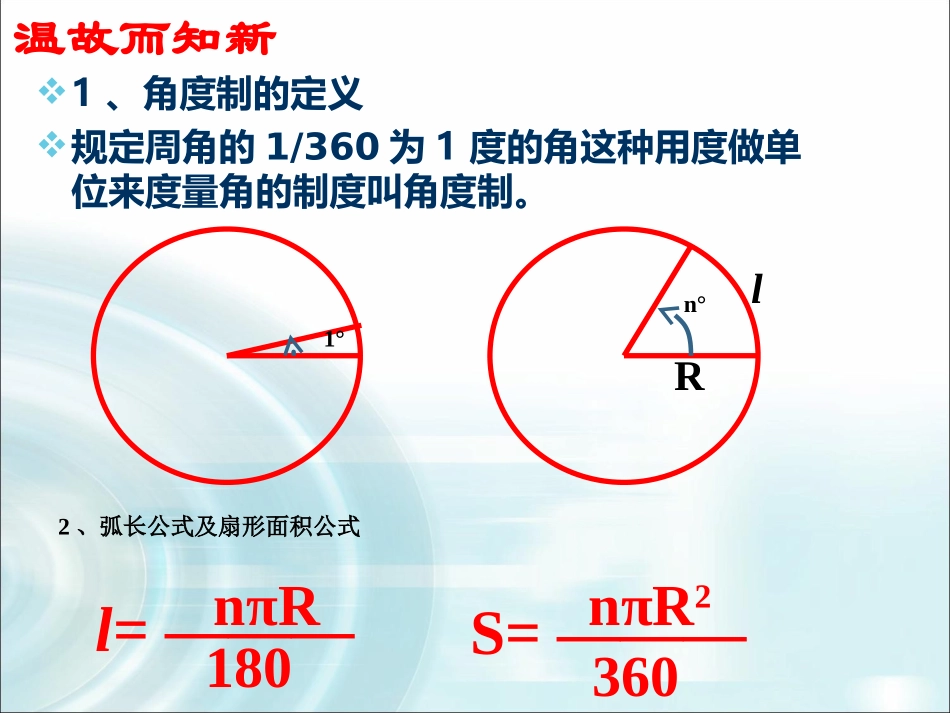
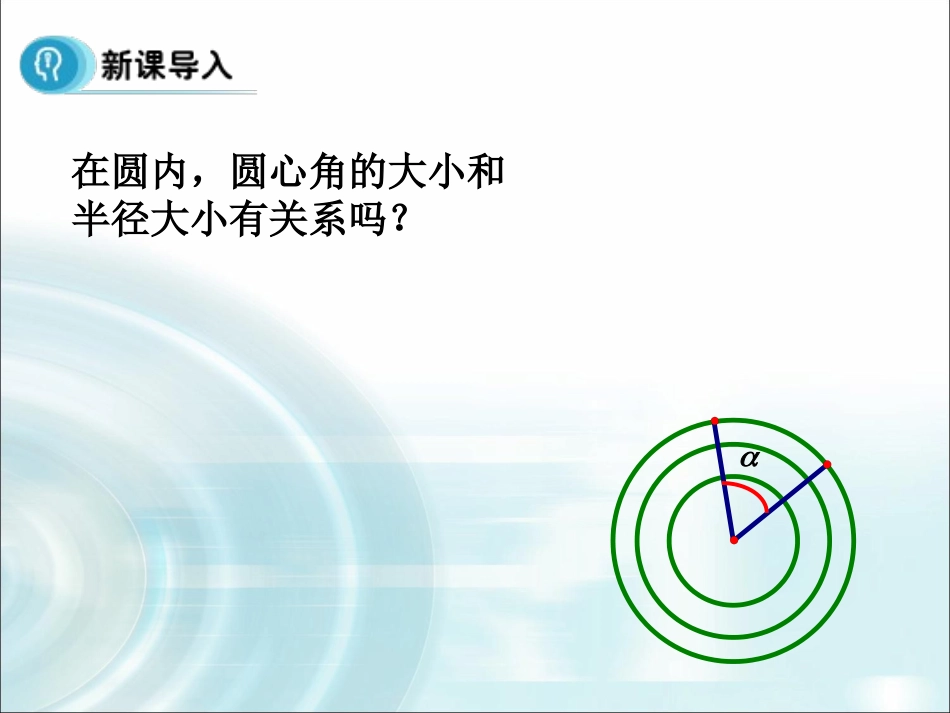
1.1.2弧度制和弧度制与角度制的换算温故而知新1、角度制的定义规定周角的1/360为1度的角这种用度做单位来度量角的制度叫角度制。1°2、弧长公式及扇形面积公式nπR180l=———nπR2360S=———n°Rl在圆内，圆心角的大小和半径大小有关系吗？1、弧度制我们把等于半径长的圆弧所对的圆心角叫做1弧度的角。设弧AB的长为l，若l=r，则∠AOB=1弧度lr=OBrl=rA1弧度讲授新课则∠AOB=2弧度lr=则∠AOB=2π弧度lr=rOABl=2r2π弧度l=2πrOA(B)r若l=2r，若l=2πr，2弧度lrOAB1.弧度：圆心角所对的弧长与半径之比称为这个角的弧度数。rl即：2.弧度制：这种以弧度作为单位来度量角的单位制叫做弧度制，它的单位是弧度，单位符号是rad.理解概念当AB弧的长度为16半径为2时正角∠AOB为多少弧度？若∠AOB为负角，且l=2r,则∠AOB为多少弧度？公式rl应该如何修改？-2rad思考:如果一个半径为r的圆的圆心角α所对的弧长是l,那么α的弧度数是多少?结论：角α的弧度数的绝对值是=lr正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零。α的正负由角α的终边旋转方向决定αradrl1.把角度换成弧度2.把弧度换成角度rad180'000185730.571801radradrad01745.018010rad23600角度制与弧度制的换算3、例题例1.把下列各角化成弧度(1)67°30'(2)120°(3)75°(4)135°(5)300°(6)-210°规律总结：833221253434355676例2:把下列各弧度化成度.(1)(2)(3)(4)53π12π54π65π(1)108o(2)15o(3)-144o(4)-150o规律总结：角度弧度0601201352704265230π645π3902π33π41501803π23600课堂练习：填定下列特殊角的度数与弧度数的对应表1、对于一些特殊角的度数与弧度数之间的换算要熟记。2.用弧度为单位表示角时，通常写成“多少π”的形式。3.弧度可以省略不写，角度不能省略。如：2与2用弧度来度量角，实际上角的集合与实数集R之间建立一一对应的关系：实数集R角的集合正角零角负角正实数零负实数对应角的弧度数其中R是半径，l是弧长，α(0<α<2π)为圆心角,S是扇形面积.例3：利用弧度制证明下列关于扇形公式:1lR2122SR132SlR证明:(1)由公式得l=αR=lr知圆心角为n°的扇形的弧长公式和面积公式分别是：2,180360nRnRlSn°转换为弧度180n212SR12SlRαradrl例4：扇形AOB中，弧AB所对的圆心角是，半径为50米，求弧AB的长60350503360rl，所以，.4,2lr解得21S4().2rlcm，，弧长为设扇形的半径为解lr,2,82rllr则有ABOlrABOlr因此扇形的面积为例5.已知扇形的周长为8厘米，圆心角为2rad，求扇形面积。1.坐标轴上的角用弧度如何表示？2.用弧度如何表示？360k例6.把下列各角化成的形式：Ζkk，202πααπ316）1（π315）2（711）3（π164143311332770723152444例.象限试判断下列各角所在的5)1(511)2(32000)3(1)4(4)5(5)1(250.5是第一象限角511)2(52511.511是第一象限角32000)3(34668320002334又.32000是第三象限角)57.1241.3(210.1是第一象限的角234.4是第三象限的角4例.象限试判断下列各角所在的1)4(4)5(（4）（5）解题思路,的角所在象限判断一个用弧度制表示一般是将其化成2()kk然的形式,.所在象限予以判断后再根据不能写成注意:(21)()kk.的形式例,33310的形式写成不能342写成而应1.的角是（）A.第一象限B.第二象限C.第三象限D.第四象限6252．若2rad的圆心角所对的弧长为4cm，则这个圆心角所对的扇形面积是()A．4cm2B．2cm2C．4πcm2D．2πcm2DA3.5弧度的角所在的象限为()A.第一象限B.第二象限C.第三象限D.第四象限D（1）弧度的定义“弧化角”时，将α乘以；（2）“角化弧”时，将n乘以；（4）（3）弧长公式：扇形面积公式：,的角所在象限判断一个用弧度制表示（1）弧度的定义“弧化角”时，将α乘以；180（2）“角化弧”时，将n乘以；180lr（3）弧长公式：21122Slrr扇形面积公式：习题1.1A组第7,8,9题．敬请指导.