复数的概念课件VIP免费

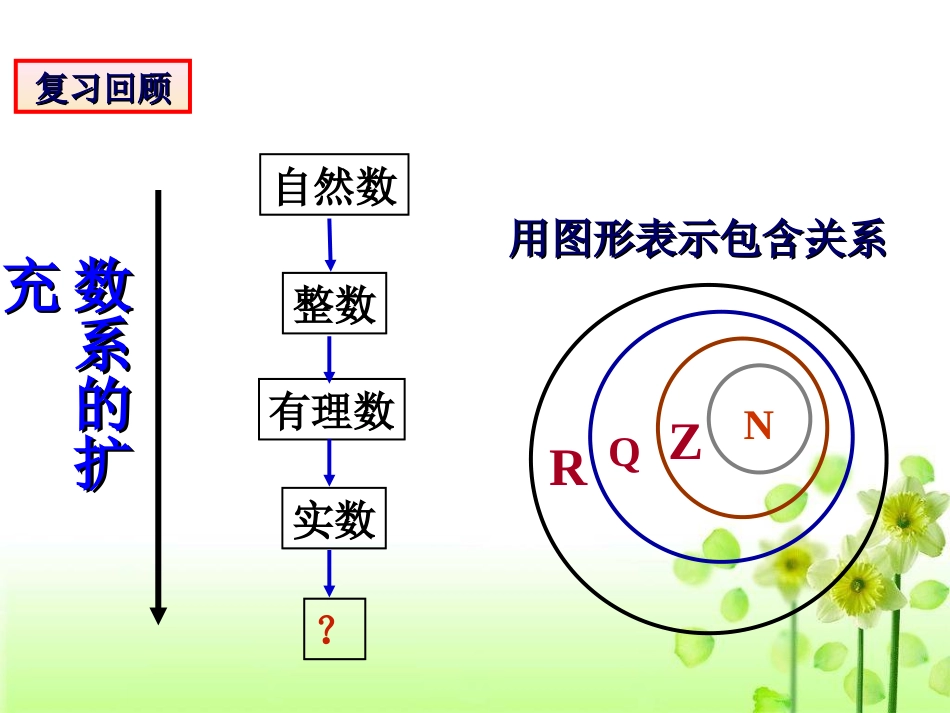
引言：在人和社会的发展过程中，常常需要立足今天，回顾昨天，展望明天。符合客观发展规律的要发扬和完善，不符合的要否定和抛弃。那么，在实数集向复数集发展的过程中，我们应该如何发扬和完善，否定和抛弃呢？数系的扩数系的扩充充自然数整数有理数实数？NZQR用图形表示包含关系：用图形表示包含关系：复习回顾复习回顾知识引入知识引入对于一元二次方程没有实数根．012x我们已知知道：我们已知知道：12x我们能否将实数集进行扩充，使得在新的数我们能否将实数集进行扩充，使得在新的数集中，该问题能得到圆满解决呢？集中，该问题能得到圆满解决呢？思考？思考？引入一个新数，叫做虚数单位，并规定：ii（1）它的平方等于－1，即12i虚数单位（2）实数可以与它进行四则运算，进行四则运算时，原有的加、乘运算律仍然成立．为了解决负数开方问题，即：将实数a和数i相加记为:a+i；把实数b与数i相乘记作:bi；将它们的和记作:a+bi(a,bR),∈全体复数所组成的集合叫复数集,用字母C表示1.复数：把形如a+bi(a,b∈R)的数叫复数i叫做虚数单位(imaginaryunit)R,,|{babiazzC其中一.复数的有关概念知识讲解知识讲解｝虚部b实部a用z表示复数,即z=a+bi(a,b∈R)叫做复数的代数形式2.复数的代数形式：规定:0i=0,0+bi=bi3.复数的分类：复数z=a+bi(a,bR)条件数的类型RC实数集R是复数集C的真子集，虚数b≠0纯虚数a=0且b≠0实数0a=b=0实数b=0复数z=a+bi(a,bR)实数(b=0)虚数(b≠0)纯虚数(a=0)非纯虚数(a≠0)1.说明下列复数是实数还是虚数，还是纯虚数？并说明各数的实部与虚部。31i31i71i2i)1(01iii)32(i2课堂练习实数虚数纯虚数纯虚数纯虚数实数实数虚数虚数2.有下列命题：（1）若a、b为实数，则z=a+bi为虚数（2）若b为实数，则z=bi必为纯虚数（3）若a为实数，则z=a一定不是虚数其中真命题的个数为（）（A）0（B）1（C）2（D）3BNZQRCNZQR思考C1.数集N，Z，Q，R，C的关系是怎样的？复数集实数集虚数集纯虚数集2.复数集，实数集，虚数集，纯虚数集之间关系4.两个复数相等有两个复数Z1=a+bi(a,bR∊)和Z2=c+di(c,dR∊)a+bi=c+dia=c且b=d注意1、若Z1,Z2均为实数,则Z1,Z2具有大小关系2、若Z1,Z2中不都为实数，Z1与Z2只有相等或不相等两关系，而不能比较大小5、共轭复数共轭复数一般地，如果两个复数的实部相等,虚部互为相反数时，这两个复数叫做互为共轭复数.,(,)zabiabR设则z=a-bi,(a,bR)例如：5+3i和5-3i互为共轭复数例1：实数m取什么值时，复数是（1）实数？（2）虚数？（3）纯虚数？immz)1(1解：（1）当，即时，复数z是实数．01m1m（2）当，即时，复数z是虚数．01m1m（3）当，且，即时，复数z是纯虚数．01m01m1m例题分析例1(补)m取何实数时，复数z＝m2－m－6m＋3＋(m2－2m－15)i(1)是实数？(2)是虚数？(3)是纯虚数？•[分析]在本题是复数的标准形式下，即z＝a＋bi(a，b∈R)，根据复数的概念，只要对实部和虚部分别计算，总体整合即可．[解析](1)当m2－2m－15＝0m＋3≠0时，m＝5或m＝－3m≠－3∴当m＝5时，z是实数．(2)当m2－2m－15≠0m＋3≠0时，即m≠5且m≠－3m≠－3∴当m≠5且m≠－3时，z是虚数．(3)当m2－m－6＝0m＋3≠0m2－2m－15≠0时，即m＝3或m＝－2m≠－3m≠5且m≠－3∴当m＝3或m＝－2时，z是纯虚数．•[点评]①判断一个含有参数的复数在什么情况下是实数、虚数、纯虚数，首先要保证参数值有意义，如果忽略了实部是含参数的分式中的分母m＋3≠0，就会酿成根本性的错误，其次对参数值的取舍，是取“并”还是“交”，非常关键，多与少都是不对的，解答后进行验算是很有必要的．•②对于复数z＝a＋bi(a，b∈R)，既要从整体的角度去认识它，把复数z看成一个整体，又要从实部与虚部的角度分解成两部分去认识它．这是解复数问题的重要思路之一．•(1)下列命题中假命题是()•A．自然数集是非负整数集•B．实数集与复数集交集为实数集•C．实数集与虚数集交集是{0}•D．纯虚数集与实数集交集为空集•[答案]C•[解析]复数可分为实数和虚数两大部分，虚数...