1.2.1任意角的三角函数VIP免费

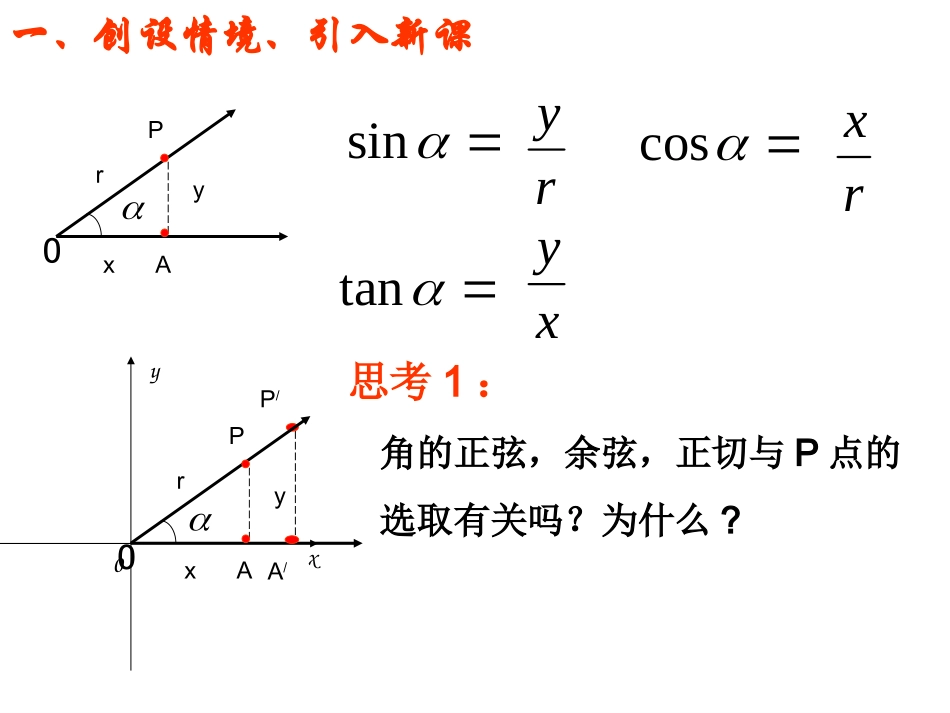
一、创设情境、引入新课OPsinAryxyrcosrxtanxy0xyP/OPAxyrA/角的正弦，余弦，正切与P点的选取有关吗？为什么?思考1：0xyOPAxyr既然在终边上选择的点位置在哪里都不影响这些三角函数的值，请问什么的改变会影响了这些三角函数的值？思考2：思考3：既然在终边上选择的点位置在哪里都不影响这些三角函数的值，那么我们现在画一个圆与角的终边有一个交点，我们就取这个点可以吗？0xyOP(x，y)sincostanxyyx这样做有什么好处？α的终边P(x，y)Oxy思考4：如果角α的终边在第二象限，那么此时的三角函数是什么？sincostanxyyx我们规定：不管角α的终边在哪个象限，它的三角函数值都为如下：注意：此时的P点选取的是终边与单位圆的交点。设是一个任意角，它的终边与单位圆交于点P(x，y)，那么：（1）y叫做的正弦，记作sin，即sin＝y（2）x叫做的余弦，记作cos，即cos＝x（3）叫做的正切（tangent），记作tan，即tan＝（x≠0）xyxy三角函数的定义P(x,y)OA(1,0)xy正弦、余弦，正切都是以角为自变量，以单位圆上点的坐标或坐标的比值为函数值的函数。以上三种函数统称三角函数．二、新课讲解例1：。的正弦、余弦和正切值求320xy方法小结：画单位圆、找交点、求比值。三、典例分析的三角函数值。求角的终边过点已知角例),-4,3(.2P方法一：画单位圆、找交点、求比值。方法二：介绍三角函数的另一种定义。rysinrxcosxytan那么),0(22yxr设角的终边上任意一点P(x,y),它与原点的距离是r·P(x,y)yOx这样定义的好处是不需要画单位圆，可直接取点求比值。的三角函数值。求角的终边过点已知角变式),0)(4,3(.1aaaP变式2.若角α的终边在直线y＝3x上，求sinα的值？的大小。求终边上一点，且是角若点变式yyP,32sin),3(3.思考5：从例1和例2两题的结果来看，我们可以看到终边在不同象限的时候其函数值的正负是不一样的。那我们能否利用刚学的定义寻找正弦、余弦、正切值在各个象限的正负情况？探究：将三种函数的值在各象限的符号填入下表+oxy（）（）（）oxy（）（）（）（）oxy（）（）（）（）sincostan口诀：一全正二正弦三正切四余弦-+-++--+--+位于哪个象限？则，想一想：如果0tan0sin例3.确定下列三角函数的符号(1)cos250°(2)(3)tan(-672°)(4))sin(43tan的值域？求xxxxxfcoscossinsin)(.2强化训练：属于第几象限？那么角属于第二象限，且满足设角2,2cos2cos.13tan23cos3sin2222）（360cos150tan90sin4270cos101）（180tan90cos0sin3cba）（例4；计算：填表角0。90。180。270。360。角的弧度数sincostan02π223π0000000011111不存在不存在。轴上，即角的终边不落在也就是说角的时候是没有意义的，在由以上可知kyxxy20tan思考6：的值一样吗？与37sin3sin如果一样你能得出一个什么结论？结论：终边相同的角的同一三角函数的值相等Zkkkk其中tan)2tan(cos)2cos(sin)2sin(即可以得到第一组诱导公式：作用:可以把任意角的三角函数化为0～2间角的三角函数;例5.求下列三角函数值:1500sin49cos)tan(611BC）是（，则且若0costan0sintan.1、第四象限角、第三象限角、第二象限角、第一象限角DCBA）三角形的形状是（则此满足、两内角若三角形,0cossin.2BABAABC、不能确定、钝角三角形、锐角三角形、直角三角形DCBA的值域？求xxxxxfcoscossinsin)(.3我们要学习三种三角函数的几何表示。0xyO0xyPMPM首先我们先来研究正弦的几何表示：sin|MP|?sin-|MP|如果我们规定与坐标轴同向的线段为正，反向为负。则此时sin象这种带有方向的线段我们把它称之为有向线段。MPsin此时xyoPMMP称之为正弦线。想一想：余弦的几何表示又是什么？McosOTA0M称之为余弦线。想一想：正切的几何表示又是什么？OMMPtan能否用一条线表示？ATOAATOMMPtanAT称之为正切线。xyoxyoxyoxyoα的终边α...