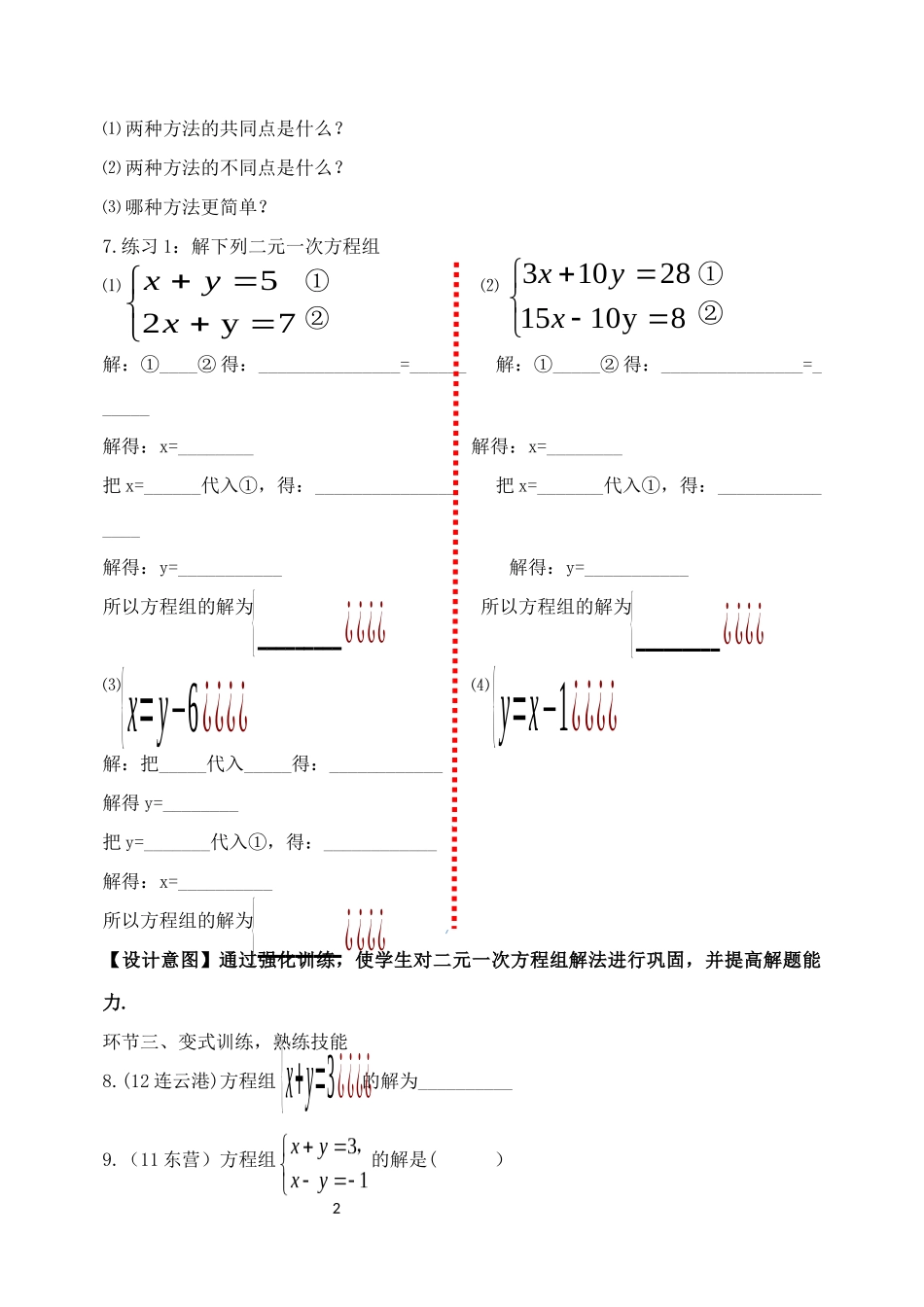
1课题:二元一次方程组的解法复习教学目标:1.理解解二元一次方程组的基本思路“消元”;2.能用代入消元法加减消元法解简单的二元一次方程组;3.会据方程组特征选择适当的方法.教学重点:理解解二元一次方程组的基本思路“消元”.教学难点:会用代入、加减消元法解简单的二元一次方程组.教学过程:环节一、知识回顾1.填空:⑴4x+(—4x)=_______;⑵3y—3y=________;⑶y+(—y)=_______;⑷—3x—(—3x)=_________;⑸—3y—(+6y)=________;⑹x-(-3x)=________2.“二元一次方程组”中的“元”是指_________________;“次”是指_______________3.解二元一次方程组的基本思路是________________4.解二元一次方程组的基本方法有___________________【设计意图】通过复习,为本节的二元一次方程组解法起到铺垫作用.环节二、解法练习:5.练习:⑴⑵你选择______消元法解此方程组最简便选择_____消元法解此方程组最简便把_____代入_____得:___________________+_____得:______________解得x=________解得x=________⑶你选择_______消元法解此方程组最简便_____―_____得:______________解得y=________6.师生总结:{x+y=6①¿¿¿¿{x+y=7①¿¿¿¿2⑴两种方法的共同点是什么?⑵两种方法的不同点是什么?⑶哪种方法更简单?7.练习1:解下列二元一次方程组⑴⑵解:①____②得:_______________=______解:①_____②得:_______________=______解得:x=________解得:x=________把x=______代入①,得:_______________把x=_______代入①,得:_______________解得:y=___________解得:y=___________所以方程组的解为所以方程组的解为⑶⑷解:把_____代入_____得:____________解得y=________把y=_______代入①,得:____________解得:x=__________所以方程组的解为【设计意图】通过强化训练,使学生对二元一次方程组解法进行巩固,并提高解题能力.环节三、变式训练,熟练技能8.(12连云港)方程组的解为__________9.(11东营)方程组的解是()7y25xyx①②8y101528103xyx①②{_________¿¿¿¿{_________¿¿¿¿{x=y−6¿¿¿¿{y=x−1¿¿¿¿{_________¿¿¿¿{x+y=3¿¿¿¿3A.B.C.D.10.(15巴中)若单项式与是同类项,则a,b的值分别为()A.a=3,b=1B.a=﹣3,b=1C.a=3,b=﹣1D.a=﹣3,b=﹣111.方程组,由②①,得正确的方程是()A.B.C.D.12.(12湛江)请写出一个二元一次方程组_________________,使它的解是13.解下列二元一次方程组⑴(10怀化)⑵(15永州)【设计意图】巩固学生对二元一次方程组解法的应用环节四、小结:问:同学们,通过这节课的学习,谈谈这节课你有什么收获?环节五、课外作业:1.(必做题)解下列二元一次方程组⑴(12广州)⑵2.(必做题)(15广州)已知a,b满足方程组,则a+b的值为()A.﹣4B.4C.﹣2D.23.(选做题)(15河北)利用加减消元法解方程组下列做法正确的是()A.要消去y,可以将①×5+②×2B.要消去x,可以将①×3+②×(﹣5)C.要消去y,可以将①×5+②×3D.要消去x,可以将①×(﹣5)+②×2【设计意图】巩固本节课所复习成果,尽量在课后有所提升.1238yxyx43125baba1131yxyx12.xy,12.xy,21.xy,01.xy,−13xa−by42x2ya+b{x−y=5¿¿¿¿