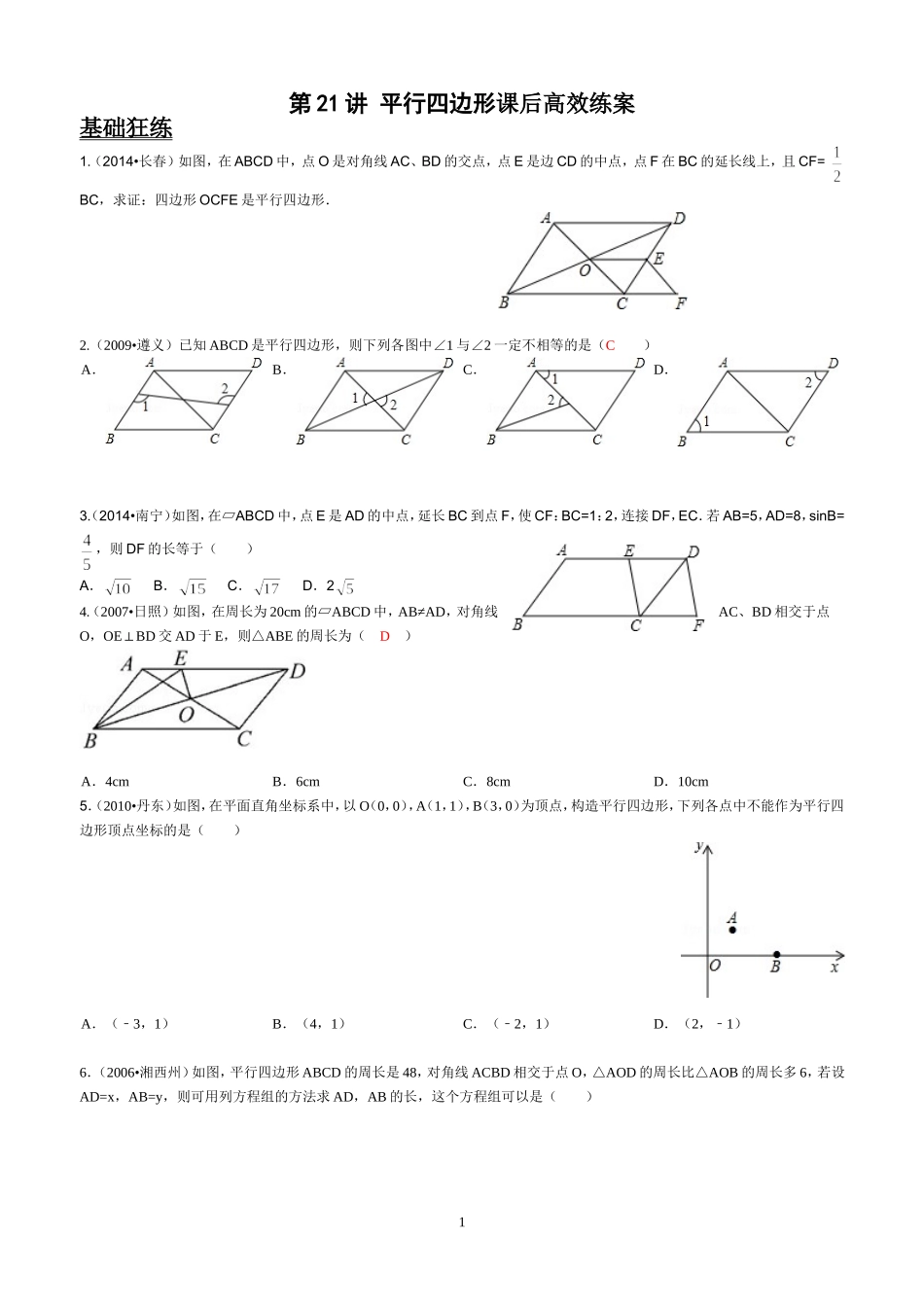
第21讲平行四边形课后高效练案基础狂练1.(2014•长春)如图,在ABCD中,点O是对角线AC、BD的交点,点E是边CD的中点,点F在BC的延长线上,且CF=BC,求证:四边形OCFE是平行四边形.2.(2009•遵义)已知ABCD是平行四边形,则下列各图中∠1与∠2一定不相等的是(C)A.B.C.D.3.(2014•南宁)如图,在▱ABCD中,点E是AD的中点,延长BC到点F,使CF:BC=1:2,连接DF,EC.若AB=5,AD=8,sinB=,则DF的长等于()A.B.C.D.24.(2007•日照)如图,在周长为20cm的▱ABCD中,AB≠AD,对角线AC、BD相交于点O,OEBD⊥交AD于E,则△ABE的周长为(D)A.4cmB.6cmC.8cmD.10cm5.(2010•丹东)如图,在平面直角坐标系中,以O(0,0),A(1,1),B(3,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形顶点坐标的是()A.(﹣3,1)B.(4,1)C.(﹣2,1)D.(2,﹣1)6.(2006•湘西州)如图,平行四边形ABCD的周长是48,对角线ACBD相交于点O,△AOD的周长比△AOB的周长多6,若设AD=x,AB=y,则可用列方程组的方法求AD,AB的长,这个方程组可以是()1A.B.C.D.7.(2008•佛山)如图,P为平行四边形ABCD的对称中心,以P为圆心作圆,过P的任意直线与圆相交于点M,N.则线段BM,DN的大小关系是(C)A.BM>DNB.BM<DNC.BM=DND.无法确定8.(2005•龙岩)如图,在▱ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于G、H,试判断下列结论:①△ABECDF≌△;②AG=GH=HC;③EG=BG;④SABE△=SAGE△,其中正确的结论是()A.1个B.2个C.3个D.4个9.(2010•綦江县)如图,在▱ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是()CDFEBC①△≌△;②∠CDF=EAF∠;③△ECF是等边三角形;④CGAE⊥.A.只有①②B.只有①②③C.只有③④D.①②③④10.(2008•潍坊)在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别AB和CD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为1,则平行四边形ABCD面积为()2A.2B.C.D.1511.(2007•嘉兴)已知△ABC的面积为36,将△ABC沿BC的方向平移到△A′B′C的位置,使B′和C重合,连接AC′交A′C于D,则△C′DC的面积为()A.6B.9C.12D.1812.(2007•黔南州)如图,在梯形ABCD中,ADBC∥,AD=5cm,BC=8cm,M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.(1)试说明△PCMQDM≌△.(2)当P在B、C之间运动到什么位置时,四边形ABPQ是平行四边形?并说明理由.13.(2005•海淀区)已知△ABC,分别以AB、BC、CA为边向形外作等边三角形ABD、等边三角形BCE、等边三角形ACF.(1)如图1,当△ABC是等边三角形时,请你写出满足图中条件,四个成立的结论;(2)如图2,当△ABC中只有∠ACB=60°时,请你证明SABC△与SABD△的和等于SBCE△与SACF△的和.14.(2014•凉山州)如图,分别以RtABC△的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EFAB⊥,垂足为F,连接DF.(1)试说明AC=EF;(2)求证:四边形ADFE是平行四边形.315.(2007•安徽)如图1,在四边形ABCD中,已知AB=BC=CD,∠BAD和∠CDA均为锐角,点P是对角线BD上的一点,PQBA∥交AD于点Q,PSBC∥交DC于点S,四边形PQRS是平行四边形.(1)当点P与点B重合时,图1变为图2,若∠ABD=90°,求证:△ABRCRD≌△;(2)对于图1,若四边形PRDS也是平行四边形,此时,你能推出四边形ABCD还应满足什么条件?(1)证明:∵∠ABD=90°,ABCR∥,CRBD∴⊥.BC=CD∵,BCR=DCR∴∠∠.∵四边形ABCR是平行四边形,BCR=BAR∴∠∠.BAR=DCR∴∠∠.又∵AB=CR,AR=BC=CD,ABRCRD∴△≌△(SAS).(2)解:由PSQR∥,PSRD∥(四边形PRDS为平行四边形)知,点R在QD上,又∵PSBC∥,PSRD∥,故BCAD∥.又由AB=CD知∠A=CDA∠,因为SRPQBA∥∥,所以∠SRD=A=CDA∠∠,从而SR=SD.由PSBC∥DCBDSP∴△∽△,BC=CD∵,SP=SD∴.而SP=DR,所以SR=SD=RD,故∠CDA=60°.因此四边形ABCD还应满足BCAD∥,∠CDA=60°.(注:若推出的条件为BCAD∥,∠BAD=60°或BCAD∥,∠BCD=120°等亦可.)4