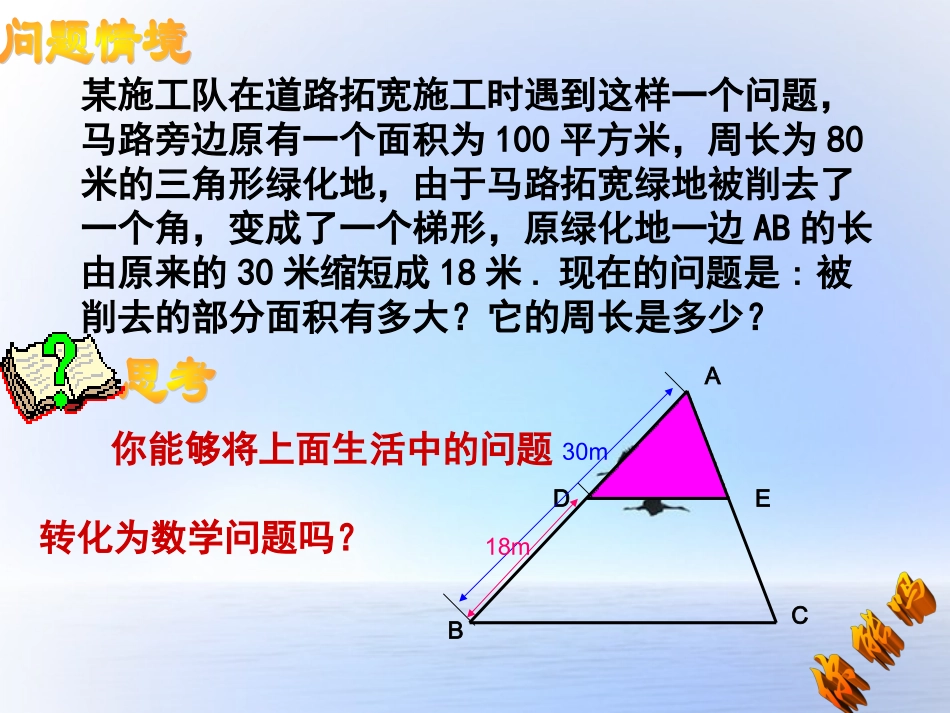
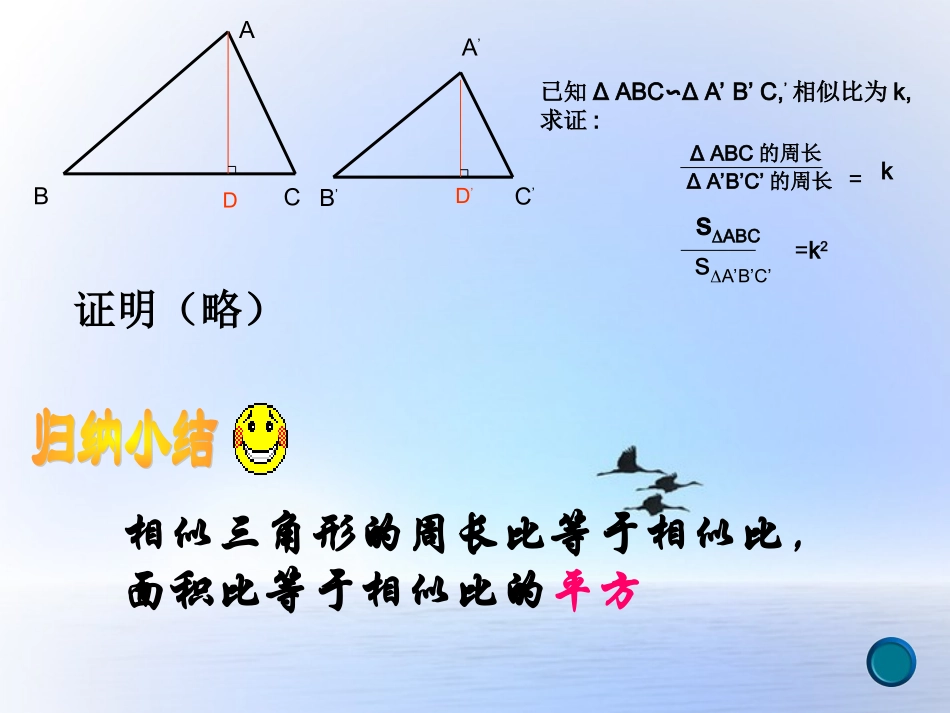
某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被削去了一个角,变成了一个梯形,原绿化地一边AB的长由原来的30米缩短成18米.现在的问题是:被削去的部分面积有多大?它的周长是多少?你能够将上面生活中的问题转化为数学问题吗?DE30m18mBCA算一算:ΔABC与ΔA’B’C’的相似比是多少?ΔABC与ΔA’B’C’的周长比是多少?面积比是多少?4×4正方形网格看一看:ΔABC与ΔA’B’C’有什么关系?为什么?验一验:是不是任何相似三角形都有此关系呢?你能加以验证吗?想一想:你发现上面两个相似三角形的周长比与相似比有什么关系?面积比与相似比又有什么关系?(相似)√22周长比等于相似比,面积比等于相似比的平方√2√102√21√5√2ABCA’C’B’ABCA’B’C’DD’证明(略)相似三角形的周长比等于相似比,面积比等于相似比的平方已知ΔABC∽ΔA’B’C,’相似比为k,求证:sABCsA’B’C’=k2ΔABC的周长ΔA’B’C’的周长=k已知:如图,△ABC∽△A’B’C’,△ABC与△A’B’C’的相似比是k,AD、A’D’是对应高。求证:kDAAD''ABCB’A’C’DD’证明:kBAABDAAD''''∵△ABCA’B’C’∽△∴∠B=B’∠∴∠ABD=A‘B’D‘=90∠O∴△ABDA’B’D’∽△已知两个三角形相似,请完成下列表格相似比周长比面积比注:周长比等于相似比,已知相似比或周长比,求面积比要平方,而已知面积比,求相似比或周长比则要开方。24100100100001913132.........例题如图:是某市部分街道图,比例尺为1:10000;请估计三条道路围成的三角形地块ABC的实际周长和面积。ABCBACDE如图,已知DE//BC,AB=30m,BD=18m,ΔABC的周长为80m,面积为100m2,求ΔADE的周长和面积30m18mADE1.过E作EF//AB交BC于F,其他条件不变,则ΔEFC的面积等于多少?BDEF面积为多少?2.若设sΔABC=S,SΔADE=S1,SΔEFC=S2.请猜想:S与S1、S2之间存在怎样的关系?你能加以验证吗?√S=√S1+√S2BCF48m236m2证明:DE//BC>ΔADE∽ΔABC>S1S=(ACAE)2EF//AB>ΔEFC∽ΔABC>S2S=ACCE()2√S>√S1=ACAE√S>√S2ACCE=}>√S√S√S2√S1+=1√S1>√S2+√S=163630m18mACBPFMNGEDS3S1S2如图,DE//BC,FG//AB,MN//AC,且DE、FG、MN交于点P。若记SΔDPM=S1,SΔPEF=S2,SΔGNP=S3SΔABC=S、S与S1、S2、S3之间是否也有类似结论?猜想并加以验证。探究1。证明:相似三角形的对应高的比,对应中线的比与对应角平分线的比等于相似比。练习1、在△ABC中,DE⁄⁄BC,E、D分别在AC、AB上,EC=2AE,则S△ADE:S四边形DBCE的比为______练习2、如图,△ABC中,DE⁄⁄FG⁄⁄BC,AD=DF=FB,则S△ADE:S四边形DFGE:S四边形FBCG=_________3.已知:梯形ABCD中,AD∥BC,AD=36,BC=60cm,延长两腰BD,CD交于点O,OF⊥BC,交AD于E,EF=32cm,则OF=_______.ABCDEFO练习4、ΔABC中,AE是角平分线,D是AB上的一点,CD交AE于G,∠ACD=∠B,且AC=2AD.则ΔACDΔ∽______.它们的相似比K=_______,______AGAEABCED1.这节课我们学到了哪些知识?2.我们是用哪些方法获得这些知识的?3.通过本节课的学习,你有没有新的想法或发现?你觉得还有什么问题需要继续讨论吗?1.作业本2.探究的推理过程课外整理完成,各组自行组织讨论交流