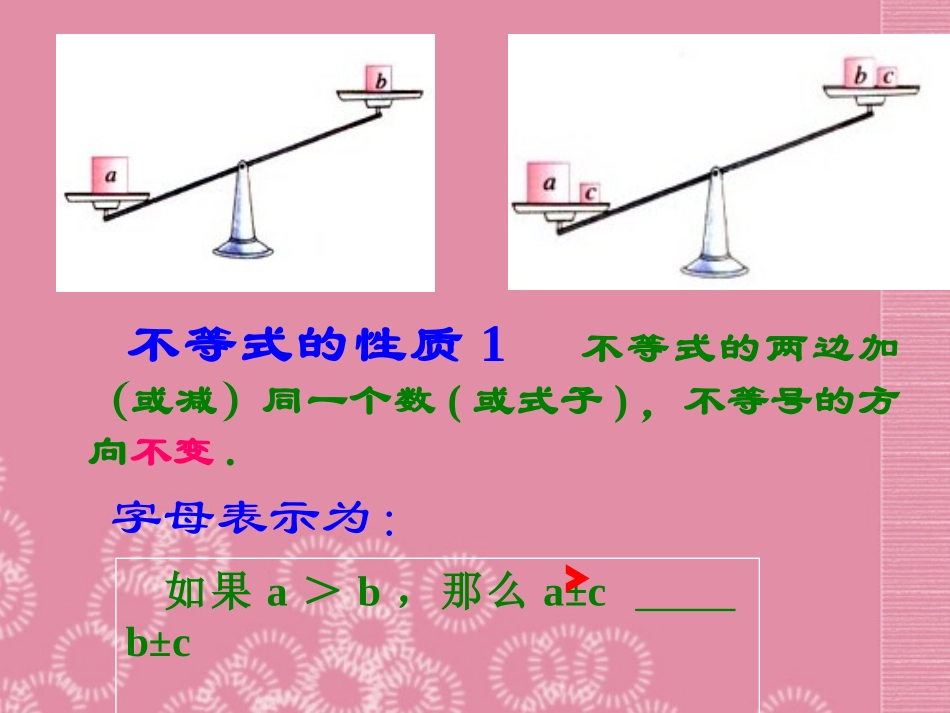
在古代,我们的祖先就懂得了翘翘板的工作原理,在古代,我们的祖先就懂得了翘翘板的工作原理,并且根据这一原理设计出了一些简单机械,并且根据这一原理设计出了一些简单机械,并把它们用到了生活实践当中.并把它们用到了生活实践当中.由此可见,“不相等”处处可见。由此可见,“不相等”处处可见。从今天起,我们开始学习一类新的数学知识:不等式.从今天起,我们开始学习一类新的数学知识:不等式.不相等处处可见11不等关系不等关系不等号的方向不等式7>4-3<47+54+5-3-74-7不变不变两边都加(或减去)同一个数不等式7>4.........根据发现的规律填空:不等式两边加(减去)同一个数(),不等号的方向()。或式子><不变不等式的性质1不等式的两边加(或减)同一个数(或式子),不等号的方向不变.如果a>b,那么a±cb±c字母表示为:﹥不等号的方向不等式7>4-8<47×54×5-8÷24÷2不变不变两边都乘(或除以)同一个正数不等式7>4.........根据发现的规律填空:不等式两边乘()同一个正数,不等号的方向()。或除以><不变不等式的性质2不等式的两边乘(或除以)同一个正数,不等号的方向不变.如果a<b,c>0那么acbc,字母表示为:﹤).___(cbca或﹤不等号的方向不等式7>4-8<47×(-5)4×(-5)-8÷(-2)4÷(-2)改变改变两边都乘(或除以)同一个负数不等式7>4.........根据发现的规律填空:不等式两边乘()同一个负数,不等号的方向()。或除以<>改变不等式的性质3不等式的两边乘(或除以)同一个负数,不等号的方向改变必须把不等号的方向改变如果a>b,c<0那么acbc,字母表示为:类比推导﹤).___(cbca或﹤不等式性质1:不等式两边加(减去)同一个正数,不等号的方向不变。不等式性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变。不等式性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变。针对练习针对练习(1)如果x-5>4,那么两边都可得到x>9(2)如果在-7<8的两边都加上9可得到(3)如果在5>-2的两边都加上a+2可得到(4)如果在-3>-4的两边都乘以7可得到(5)如果在8>0的两边都乘以8可得到(6)如果在的两边都乘以14可得到X7>2+X2加上52<17a+7>a-21>-2864>02x>28+7x(1)如果在不等式8>0的两边都乘以―8可得到(2)如果-3x>9,那么两边都除以―3可得到(3)设m>n,用“>”或“<”填空:m-5n-5(根据不等式的性质)-6m-6n(根据不等式的性质)针对练习-64<0x<-3>1<3例1利用不等式的性质解下列不等式用数轴表示解集.(1)x-7>264344x我是最棒的☞☞解:根据不等式性质1,得X-7+7>26+7X>33330(2)-4x3﹥解:根据不等式性质3,得X<―43解未知数为x的不等式,就是要使不等式逐步化为xa﹥或xa﹤的形式.043(3)3x<2x+13x-2x2x+1-2xx﹤1﹤这个不等式的解在数轴上的表示01解:根据不等式性质1,得3x-2x1﹤自我检测利用不等式的性质解下列不等式用数轴表示解集.(1)x+3>-1解:根据不等式性质1,得6X-5X<5X-7-5XX<-7(3)4x>-12解:根据不等式性质2,得X>-30-4-700-3解:根据不等式性质1,得X+3-3>-1-3X>-4(2)6x<5x-72(4)-x50﹥3x75﹥这个不等式的解集在数轴的表示如图075解:2为了使不等式-x50﹥中不等号的一边变为x,根据不等式的性质2,不等式的两边都乘不等号的方向不变,得332将未知数系数化1452615xx(4)解:不等式两边同时乘以12,得2(5x+1)-2×12>3(x-5)10x+2-24>3x-1510x-3x>24-2-157x>7X>1去分母拆括号移项合并同类项系数化101新情境题以下不等式中,不等号用对了么?(1)3-a<6-a(2)3a<6a解:(1)3<6,根据不等式的性质1将不等式两边同时减a,3-a<6-a(2)3<6,当a>0时,根据不等式的性质2,3a<6a当a<0时,根据不等式的性质3,3a>6a如果关于x的不等式(1-a)x>1-a的解集为x<1,那么请给出一个符合题意a的值解:由(1-a)x>1-a,不等式两边同时除以1-a,得到x<1不等号方向改变了,由不等式的性质3可知1-a<0,a>1可以取a=2作业:P128-----3,6图图'图图图'Authorware文文'[文文文]'文文1文文,4K文文2008文5文3文