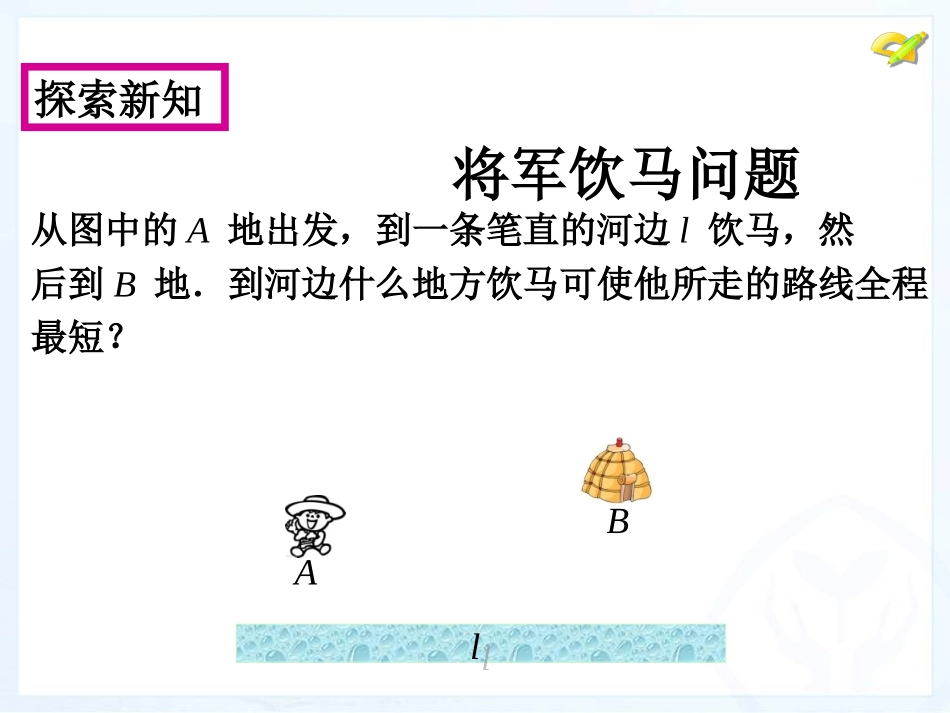
八年级上册13.4课题学习最短路径问题如图所示,从A地到B地有三条路可供选择,你会选走哪条路最近?你的理由是什么?两点之间,线段最短FEDCBA①②③将军饮马问题从图中的A地出发,到一条笔直的河边l饮马,然后到B地.到河边什么地方饮马可使他所走的路线全程最短?探索新知BAll你能将这个问题抽象为数学问题吗?探索新知BAll追问1这是一个实际问题,你打算首先做什么?将A,B两地抽象为两个点,将河l抽象为一条直线.探索新知B··Al追问1对于问题2,如何将点B“移”到l的另一侧B′处,满足直线l上的任意一点C,都保持CB与CB′的长度相等?探索新知问题2如图,点A,B在直线l的同侧,点C是直线上的一个动点,当点C在l的什么位置时,AC与CB的和最小?B·lA·追问2你能利用轴对称的有关知识,找到上问中符合条件的点B′吗?探索新知问题2如图,点A,B在直线l的同侧,点C是直线上的一个动点,当点C在l的什么位置时,AC与CB的和最小?B·lA·作法:(1)作点B关于直线l的对称点B′;(2)连接AB′,与直线l相交于点C.则点C即为所求.探索新知问题2如图,点A,B在直线l的同侧,点C是直线上的一个动点,当点C在l的什么位置时,AC与CB的和最小?B·lA·B′B′CC探索新知问题3你能用所学的知识证明AC+BC最短吗?B·lA·B′B′CC证明:如图,在直线l上任取一点C′(与点C不重合),连接AC′,BC′,B′C′.由轴对称的性质知,BC=B′C,BC′=B′C′.∴AC+BC=AC+B′C=AB′,AC′+BC′=AC′+B′C′.探索新知问题3你能用所学的知识证明AC+BC最短吗?B·lA·B′B′CCC′C′探索新知问题3你能用所学的知识证明AC+BC最短吗?B·lA·B′B′CCC′C′证明:在△AB′C′中,AB′<AC′+B′C′,∴AC+BC<AC′+BC′.即AC+BC最短.若直线l上任意一点(与点C不重合)与A,B两点的距离和都大于AC+BC,就说明AC+BC最小.探索新知B·lA·B′B′CCC′C′追问1证明AC+BC最短时,为什么要在直线l上任取一点C′(与点C不重合),证明AC+BC<AC′+BC′?这里的“C′”的作用是什么?探索新知追问2回顾前面的探究过程,我们是通过怎样的过程、借助什么解决问题的?B·lA·B′B′CCC′C′运用新知练习如图,一个旅游船从大桥AB的P处前往山脚下的Q处接游客,然后将游客送往河岸BC上,再返回P处,请画出旅游船的最短路径.AABBCCPPQQ山山河岸河岸大桥大桥运用新知基本思路:由于两点之间线段最短,所以首先可连接PQ,线段PQ为旅游船最短路径中的必经线路.将河岸抽象为一条直线BC,这样问题就转化为“点P,Q在直线BC的同侧,如何在BC上找到一点R,使PR与QR的和最小”.基本思路:由于两点之间线段最短,所以首先可连接PQ,线段PQ为旅游船最短路径中的必经线路.将河岸抽象为一条直线BC,这样问题就转化为“点P,Q在直线BC的同侧,如何在BC上找到一点R,使PR与QR的和最小”.AABBCCPPQQ山山河岸河岸大桥大桥问题2(造桥选址问题)如图,A和B两地在一条河的两岸,现要在河上建一座桥MN,桥造在何处才能使从A到B的路径AMNB最短?(假设河的两岸是平行的直线,桥要与河垂直)我们能否在不改变AM+MN+BN的前提下把桥转化到一侧呢?什么图形变换能帮助我们呢?思维火花问题解决BAA1MN如图,平移A到A1,使AA1等于河宽,连接A1B交河岸于N作桥MN,此时路径AM+MN+BN最短.理由;另任作桥M1N1,连接AM1,BN1,A1N1.N1M1由平移性质可知,AM=A1N,AA1=MN=M1N1,AM1=A1N1.AM+MN+BN转化为AA1+A1B,而AM1+M1N1+BN1转化为AA1+A1N1+BN1.在△A1N1B中,由线段公理知A1N1+BN1>A1B因此AM1+M1N1+BN1>AM+MN+BN•2.如图:牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到帐篷B,请你帮他确定这一天的最短路线。作法:1.作点A关于直线MN的对称点点F,2.作点B关于直线L的对称点点E,3.连接EF分别交直线OA.OB于点G.H,则AG+GH+BH最短FMNlB··AEGH归纳小结(1)本节课研究问题的基本过程是什么?(2)轴对称在所研究问题中起什么作用?(1)本节课研究问题的基本过程是什么?(2)轴对称在所研究问题中起什么作用?