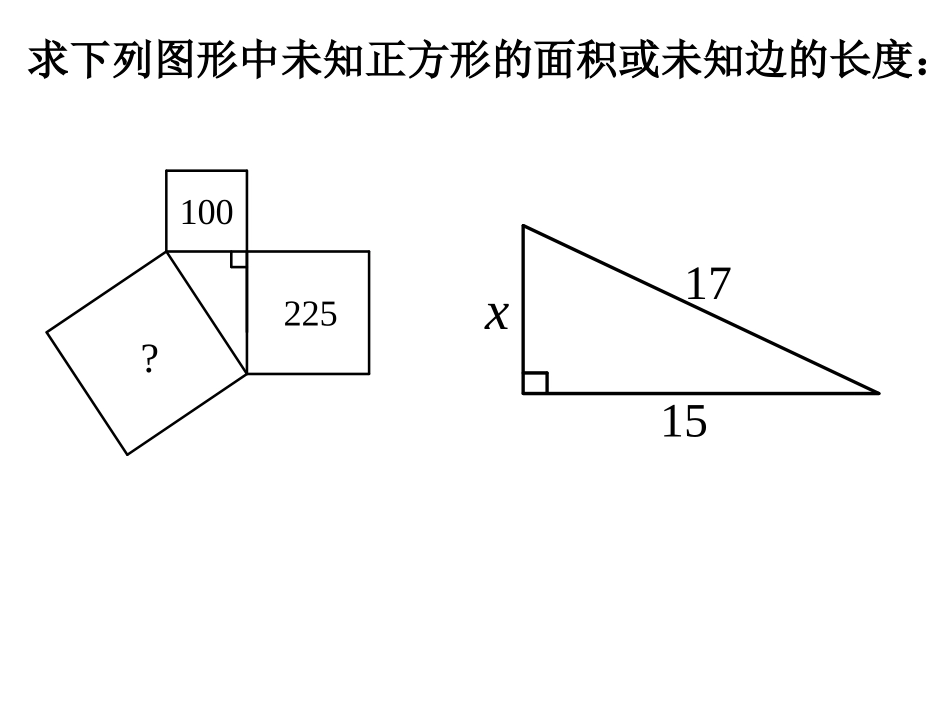
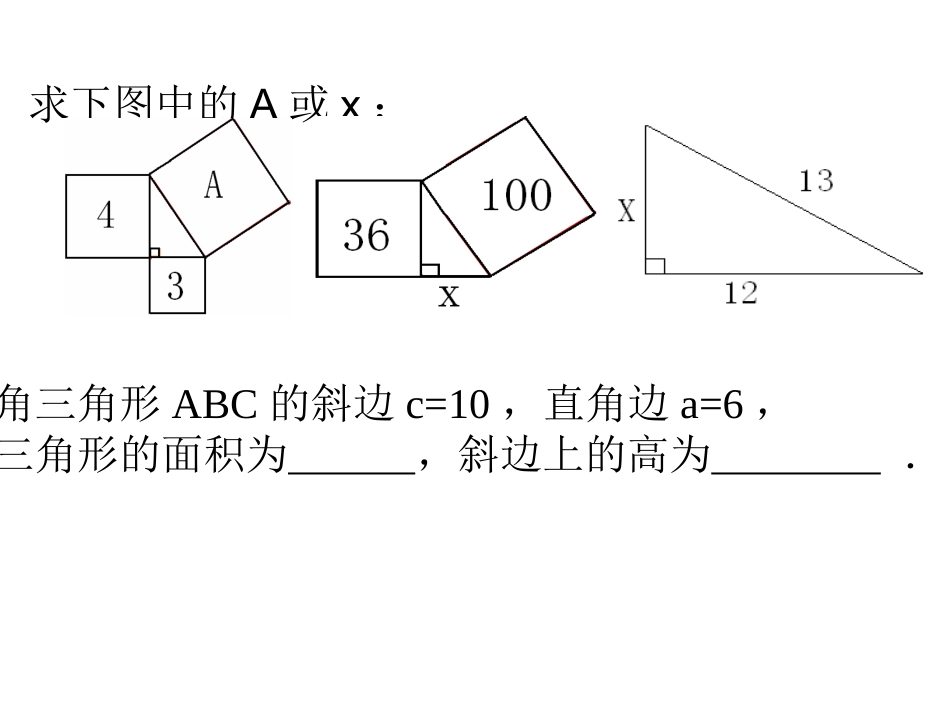
求下列图形中未知正方形的面积或未知边的长度:?225100x1517求下图中的A或x:直角三角形ABC的斜边c=10,直角边a=6,则三角形的面积为,斜边上的高为.做一做:在△ABC中,∠C=90°,(1)若a=7,c=25,则b=_______.(3)若CDAB⊥,a=10,b=24,则CD=______.(2)若a:b=3:4,c=20,则a=_____,b=______.ABC1.△ABC中,AB=AC=20cm,BC=32cm.求△ABC面积.D刘徽刘徽,(生于公元250年左右),三国后期魏国人,是中国古代杰出的数学家,也是中国古典数学理论的奠基者之一.无字证明青出朱方青方朱入朱出青入青入青出青出abc无字证明无字证明①②③④⑤青出朱入朱出朱方青方青入青入青出青出华罗庚青朱出入图朱入朱出五巧板的制作ABCEDFGHI①②③④⑤abc1.用两副五巧板,将其中的一副拼成一个以c为边长的正方形;将另一副拼成两个边长分别为a、b的正方形。你拼出来了吗?你能验证勾股定理了吗?组成、、由小正方形组成;、由小正方形组成;、、、、由大正方形如图5422312543212::::6SSSbSSaSSSSSc222cba故1122334455图6acb2.用上面的两副五巧板,还可以拼出如下所示的图形:组成、、由小正方形组成;、由小正方形组成;、、、、由大正方形如图5422312543212::::7SSSbSSaSSSSSc222cba故122334455图7acb3.用上面的五巧板,还可以拼出“青朱出入图”。刘徽在他的《九章算术》中给出了注解,大意是:三角形ABC为直角三角形,以勾为边的正方形为朱方,以股为边的正方形为青方;以盈补虚,将朱、青二方并成弦方,依面积关系有,由于朱方、青方各有一部分在弦方内,那一部分就不动了。222cba青方朱出朱方青入青出青出青入abcABC图8朱入意大利文艺复兴时代的著名画家达·芬奇对勾股定理也曾进行了研究,他验证勾股定理的方法可以从下面的实验中得到体现:1.在一张长方形的纸板上画两个边长分别为a、b的正方形,并连结BC、EF,如图9所示;OCABEFba图9OCABEFba图9ⅡⅠA’B’C’D’E’F’图10图112.沿ABCDEFA剪下,得到两个大小相同的纸板Ⅰ、Ⅱ如图10所示;3.将纸板Ⅱ翻转后与Ⅰ拼成如图11所示的图形;4.比较图9、图11中两个多边形ABCDEF和ABCDEF的面积,你能验证勾股定理吗?让学生相互交流、讨论、合作,利用面积关系可得到:SABCDEF=SA’B’C’D’E’F’abcbaba212212222即abcbaba222222acb故OCABEFba图9ⅡⅠA’B’C’D’E’F’图10图11如图,将长为2.5米的梯子AC斜靠在墙上,BC长为0.7米,求:(1)梯子上端A到墙的底端B的距离AB。ACBA`C`0.4m(梯子长度不变2)如果梯子上端A向下滑动0.4米到A′处,则梯子的底端C向C′是否也滑动了0.4米,如果是,请说明理由;如果不是,请说出滑动了多少米?