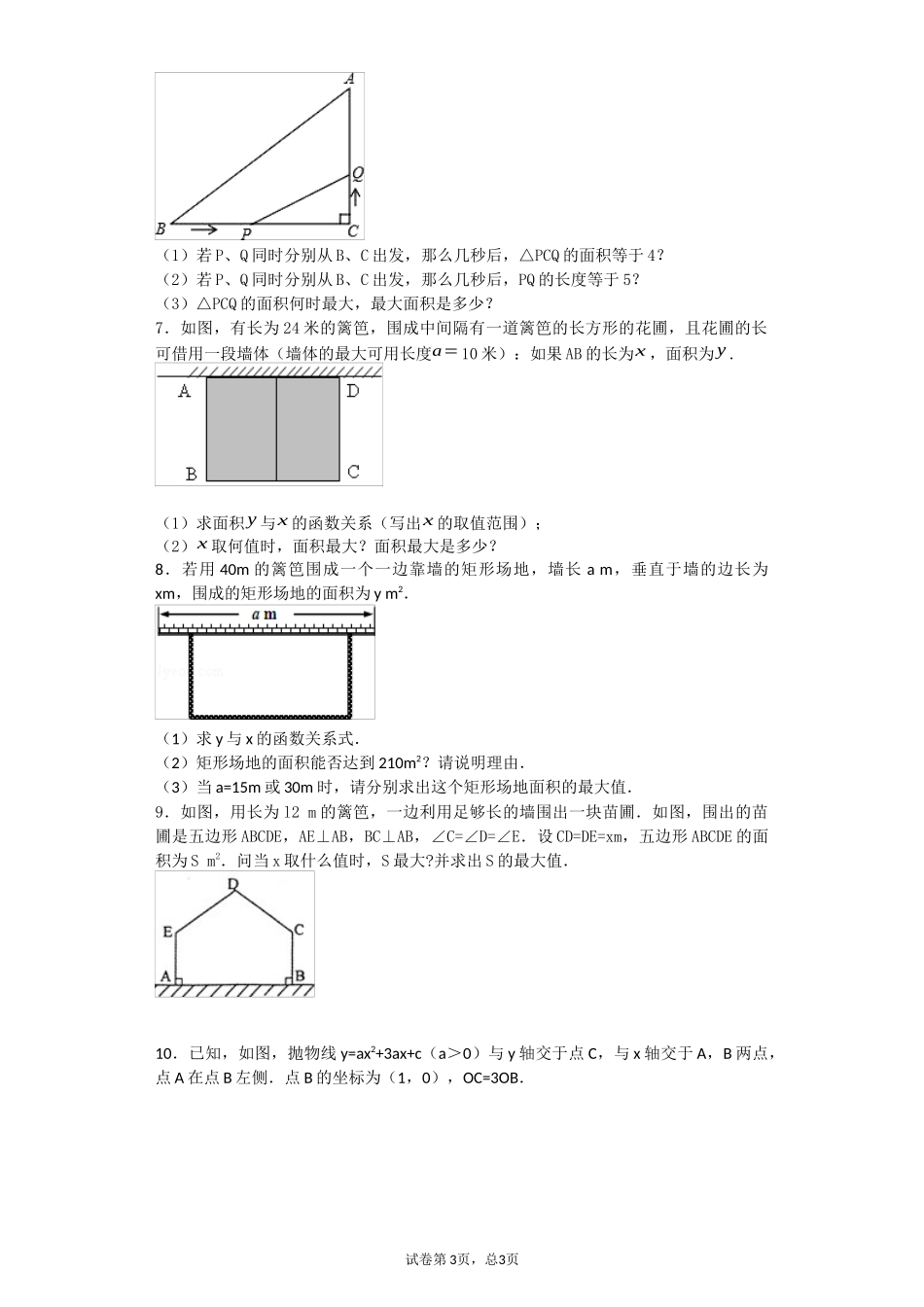
初四数学二次函数中的最大面积专题练习题1.如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC.抛物线y=ax2+bx+c经过点A、B、C.(1)求抛物线的解析式.(2)若点P是第二象限内抛物线上的动点,其横坐标为t.①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时点P的坐标.②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD面积的最大值;若不存在,请说明理由.2.如图,已知抛物线y=ax2−32x+c与x轴相交于A,B两点,并与直线y=12x−2交于B,C两点,其中点C是直线y=12x−2与y轴的交点,连接AC.(1)求抛物线的解析式;(2)证明:△ABC为直角三角形;(3)△ABC内部能否截出面积最大的矩形DEFG?(顶点D、E、F、G在△ABC各边上)若能,求出最大面积;若不能,请说明理由.3.某基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长54米的不锈钢栅栏围成,与墙平行的一边留一个宽为2米的出入口,如图所示,如何试卷第1页,总3页设计才能使园地的而积最大?下面是两位学生争议的情境:请根据上面的信息,解决问题:(1)设AB=x米(x>0),试用含x的代数式表示BC的长;(2)请你判断谁的说法正确,为什么?4.如图,已知抛物线y=ax2+bx+c过点A(6,0),B(-2,0),C(0,-3).(1)求此抛物线的解析式;(2)若点H是该抛物线第四象限的任意一点,求四边形OCHA的最大面积;(3)若点Q在y轴上,点G为该抛物线的顶点,且∠QGA=45º,求点Q的坐标.5.如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.(1)求A、B、C的坐标;(2)设点H是第二象限内抛物线上的一点,且△HAB的面积是6,求点H的坐标;(3)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积.6.如图,△ABC中,∠C=90°,BC=7cm,AC=5,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动.试卷第2页,总3页(1)若P、Q同时分别从B、C出发,那么几秒后,△PCQ的面积等于4?(2)若P、Q同时分别从B、C出发,那么几秒后,PQ的长度等于5?(3)△PCQ的面积何时最大,最大面积是多少?7.如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借用一段墙体(墙体的最大可用长度a=10米):如果AB的长为x,面积为y.(1)求面积y与x的函数关系(写出x的取值范围);(2)x取何值时,面积最大?面积最大是多少?8.若用40m的篱笆围成一个一边靠墙的矩形场地,墙长am,垂直于墙的边长为xm,围成的矩形场地的面积为ym2.(1)求y与x的函数关系式.(2)矩形场地的面积能否达到210m2?请说明理由.(3)当a=15m或30m时,请分别求出这个矩形场地面积的最大值.9.如图,用长为l2m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=xm,五边形ABCDE的面积为Sm2.问当x取什么值时,S最大?并求出S的最大值.10.已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.试卷第3页,总3页(1)求抛物线的解析式;(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.11.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.(1)求这个二次函数的表达式;(2)当点P运动到什么位置时,△BPC的面积最大?求出此时P点的坐标和△BPC的最大面积;(3)连接PO、PC,并把△POC沿CO翻折,得到四边形POP1C,那么是否存在点P,使四边形POP1C为菱形?若存在,直接写出此时点P的坐标;若不存在,请说明理由.12.课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm...