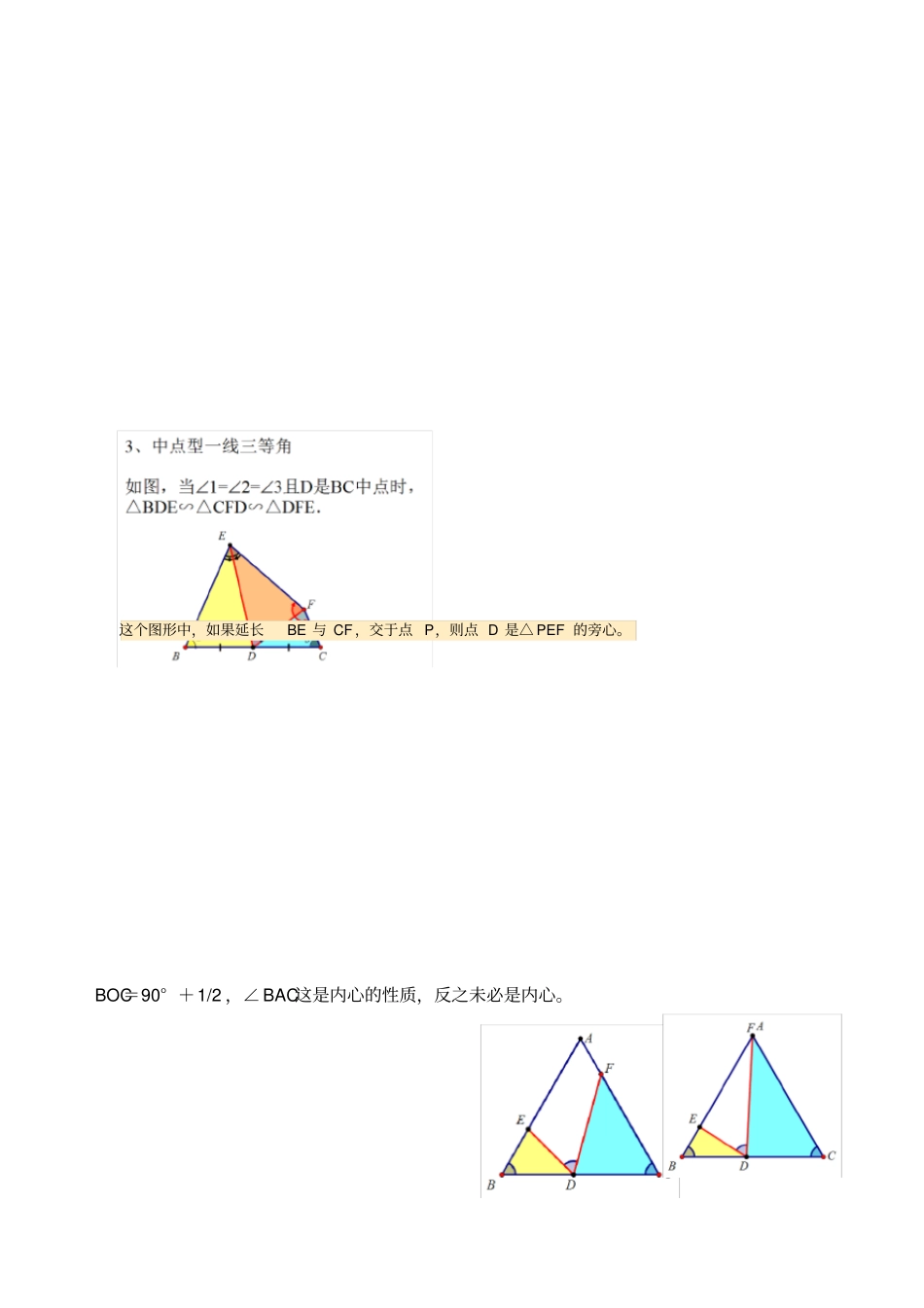
一线三等角是一个常见的相似模型,指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。不同地区对此有不同的称呼,义乌通常称为“K形图”,哈尔滨通常称为“M形图”,以下统称为“一线三等角”。在义乌,主要是一线三直角,几乎是每年必考的压轴题早期出现的一线三等角以上面这两种形式呈献的较多这个图形中,如果延长BE与CF,交于点P,则点D是△PEF的旁心。BOC=90°+1/2,∠BAC这是内心的性质,反之未必是内心。以等腰三角形为例进行说明下面这种比较少见些其实这个延长DC反而好理解相当于两侧型的不延长理解累,以为是一种新型的同侧穿越型?不管怎么变,都是由三等角确定相似三角形来进行解题感觉最后一种情况出现得比较多,尤其是压轴大题中,经常会有一个特殊角或者知道三角函数值的角时,我经常构造一线三等角来解题坐标系中,要讲究“线”的特殊性特别是定线如图,线上有一特殊角,就考虑构造同侧型一线三等角尤其是坐标轴或平行坐标轴为三等角的"线"当然只加这两条线通常是不够的,为了利用这个特殊角导线段的关系,过C、D两点作直线l的垂线是必不可少的上面就是作辅助线的一般程序,看起来线条比较多,很多老师都认为一下子不容易掌握苏德杰:多一对相似,可利用的结论又多了,解决题目的机会增大喽刘俊勇:根据我的经验,经过训练之后,学生掌握得还是比较快的于新华:两条垂线通常情况下是为了“量化”的需要。漳平林福凯:外弦图较易掌握并应用,内弦图得再加思悟领会,使得内丶外弦图一致化漳平林福凯:两条垂线通常情况下是为了“量化”的需要。于特总估本质,经典刘俊勇:来看一个简单的题,初二学生的这个容易的就不多讲了,对学生来说分类讨论是难点这个题很经典,请大家构造一下上海姜箐羿:作以A为真角顶点,C在斜边上的等腰三角形刘俊勇:这个题目传统和一线三等角都可,方法多多天涯:我想到的是倍角共顶点旋转模型浙江曹天:遇到特殊角,一般都可以构造马鞍山周明和:有没有优化的可能呢?一线三等构成主要依据是什么?黄裳元吉:角相等,构等角刘俊勇:BC这条线上有个45°的特殊角,可以分别过A、D点构造同侧型一线三等角这种辅助线很程式化,不需要动多少脑子,掌握以后中上学生也可以较快做这样的题江苏于新华:会者不难,难者不会刘俊勇:效果如下黄裳元吉:其实此题也可以用一线等三角形,加中点模型秒杀!河南敖勇:BC这条线上有个45°的特殊角,可以分别过A、D点构造同侧型一线三等角这是要点刘俊勇:在坐标系中,主要考虑在坐标轴上或与坐标轴平行的线上构造一线三等角基于此,刚才这个还可以在水平线上构造江苏于新华:听讲座是一方面,一定要练习,要模仿,只有体会到成就感后,你才会一直想这样用,从而熟练了,也就形成技能了。光听不练是没有效果的。刘俊勇:江苏姜鸿雁:这是这么想的重要依据!这么想比怎么做重要。离开大背景,想到解决策略,比什么都重要。(线上有45度角)】刘俊勇:下面这种构造也可以:这个不容易想到些盐城树伟:围绕45做文章徐州汤杰:一线三等角,神在会构造安徽阜阳刘国超:依据是什么?常州何平:斜线上构造最难刘俊勇:当然此题的正解我觉得还是母子相似浙江曹天:构造一线三等角本质在于能够定型!刘俊勇:依据在有特殊角山东齐欣:借助一线三等角构造相似三角形实现边角关系转化,很好的素材;体现了数学的育人价值那个等边三角形的问题,用“捆绑旋转”作图法也是非常简单的。