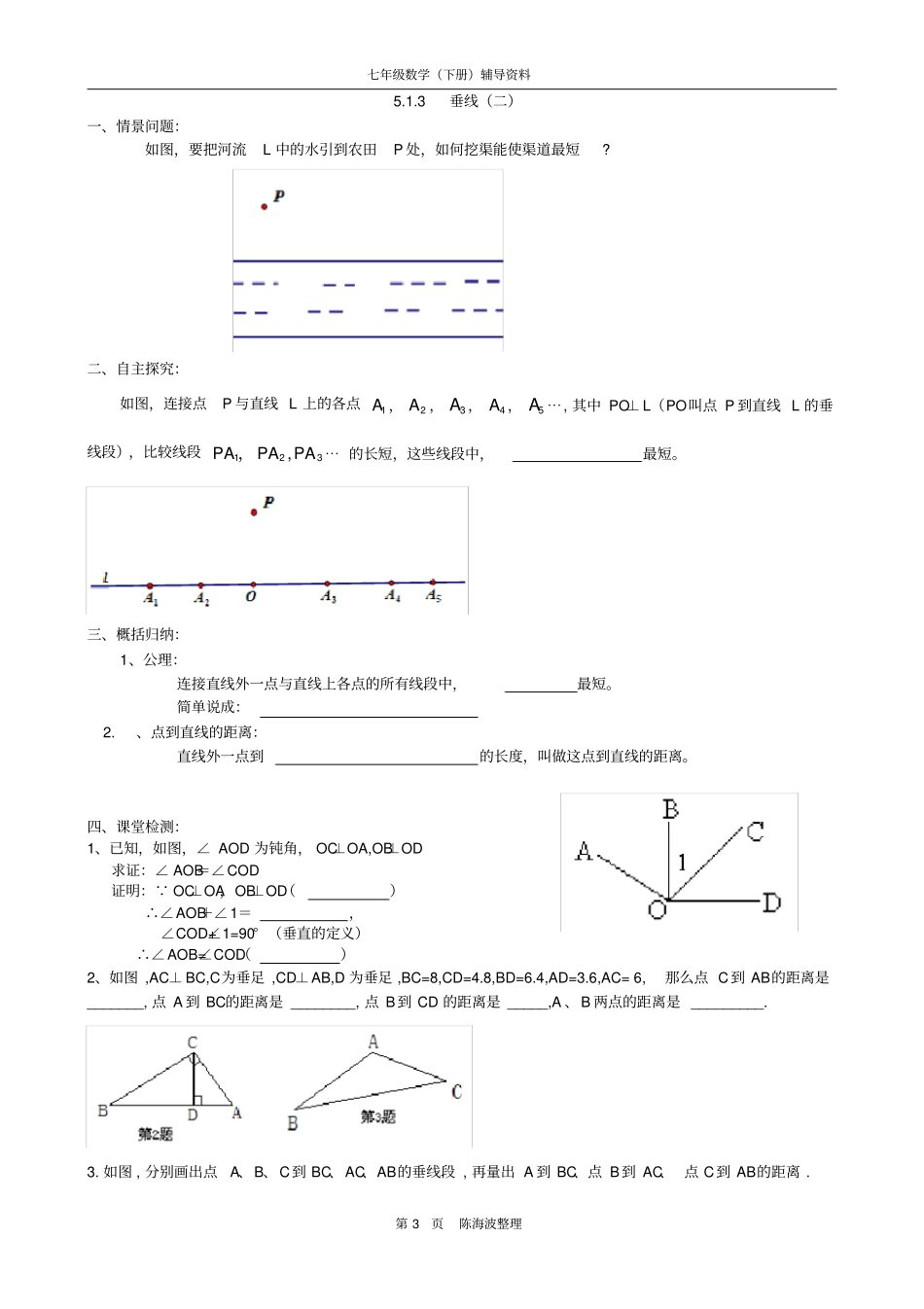
七年级数学(下册)辅导资料第1页陈海波整理第五章相交线与平行线5.1.1相交线一、自主探究1、填一填两直线相交所形成的角分类位置关系数量关系4321ODCBA2、想一想:绕点O旋转直线AB,所形成的四个角的大小变了吗?每两个角之间的关系变了吗?二、概括归纳1、邻补角概念:,这样的两个角叫互为邻补角;请指出上图中的邻补角:性质:2、.对顶角概念:,这样的两个角叫互为对顶角;三、课堂检测:1、如图,直线AB、CD、EF相交于点O,∠BOE的对顶角是_______,∠COF的邻补角是________.若∠AOC:∠AOE=2:3,∠EOD=130°,则∠BOC=_________.FEODCBA2、如图,直线AB、CD相交于点O.(1)若∠AOC+∠BOD=100°,求各角的度数.(2)若∠BOC比∠AOC的2倍多33°,求各角的度数5.1.2垂线(一)1、如图,若∠1=60°,那么∠2=、∠3=、∠4=.2、改变上图中∠1的大小,若∠1=90°,请画出这种图形,并求出此时∠2=、∠3=、∠4的大小。上面所画图形中两条直线的关系是__________,知道两条直线互相________是两条直线相交的特殊情况。2、用语言概括垂直定义两条直线相交,所成四个角中有一个角是_____时,我们称这两条直线__________其中一条直线是另一条的_____,他们的交点叫做_____。3、垂直的表示方法:垂直用符号“⊥”来表示,若“直线AB垂直于直线CD,垂足为O”,则记为__________________ODCBA七年级数学(下册)辅导资料第2页陈海波整理ODCBACEAOBFD4、垂直的推理应用:(1) ∠AOD=90°()∴AB⊥CD()(2) AB⊥CD()∴∠AOD=90°()画图实践:1.用三角尺或量角器画已知直线L的垂线.(1)已知直线L,画出直线L的垂线,能画几条?L小组内交流,明确直线L的垂线有_________条,即存在,但位置有不______性。(2)怎样才能确定直线L的垂线位置呢?在直线L上取一点A,过点A画L的垂线,能画几条?再经过直线L外一点B画直线L的垂线,这样的垂线能画出几条?B..LLA从中你能得出什么结论?____________________________________________.二、检测:1、如图,直线AB、EF相交于O点,CDAB于O点,EOD12819,BOFAOF,的度数分别为.2、(1)画图:①直线AB、CD相交于点O②过O点作OE⊥CD于O,并使OE、OB在CD的同侧。(2)若有∠BOE=31∠BOC,求∠AOC的度数。3、.已知钝角∠AOB,点D在射线OB上.(1)画直线DE⊥OB(2)画直线DF⊥OA,垂足为F.七年级数学(下册)辅导资料第3页陈海波整理5.1.3垂线(二)一、情景问题:如图,要把河流L中的水引到农田P处,如何挖渠能使渠道最短?二、自主探究:如图,连接点P与直线L上的各点1A,2A,3A,4A,5A⋯,其中PO⊥L(PO叫点P到直线L的垂线段),比较线段321,PAPAPA,⋯的长短,这些线段中,最短。三、概括归纳:1、公理:连接直线外一点与直线上各点的所有线段中,最短。简单说成:2.、点到直线的距离:直线外一点到的长度,叫做这点到直线的距离。四、课堂检测:1、已知,如图,∠AOD为钝角,OC⊥OA,OB⊥OD求证:∠AOB=∠COD证明: OC⊥OA,OB⊥OD()∴∠AOB+∠1=,∠COD+∠1=90°(垂直的定义)∴∠AOB=∠COD()2、如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC=6,那么点C到AB的距离是_______,点A到BC的距离是________,点B到CD的距离是_____,A、B两点的距离是_________.3.如图,分别画出点A、B、C到BC、AC、AB的垂线段,再量出A到BC、点B到AC、点C到AB的距离.七年级数学(下册)辅导资料第4页陈海波整理5.1.2同位角、内错角和同旁内角一、探索新知:1、我们知道,两条直线相交形成个角,每两个角之间是或关系。2、如图,两条直线a,b都与第三条直线c相交(也可说两条直线a,b被第三条直线c所截)形成个角。其中有公共顶点的两个角是邻补角或没有公共顶点的两个角是什么关系?二、概括归纳:1、.同位角:像∠1和∠5这样,分别位于直线a,b的,并且都在直线c的,具有这样关系的一对角叫同位角。(图中还有同位角是)2、内错角:像∠3和∠5这样,分别位于直线a,b,并且分别在直线c的,具有这样关系的一对角叫内错角。(图中还有内错角是)3、同旁内角:像∠4和∠5这样,分别位于直线a,b的,并且都在直线c的,具有这样关系的一对角叫同旁内角。(图中还有同旁内角是...