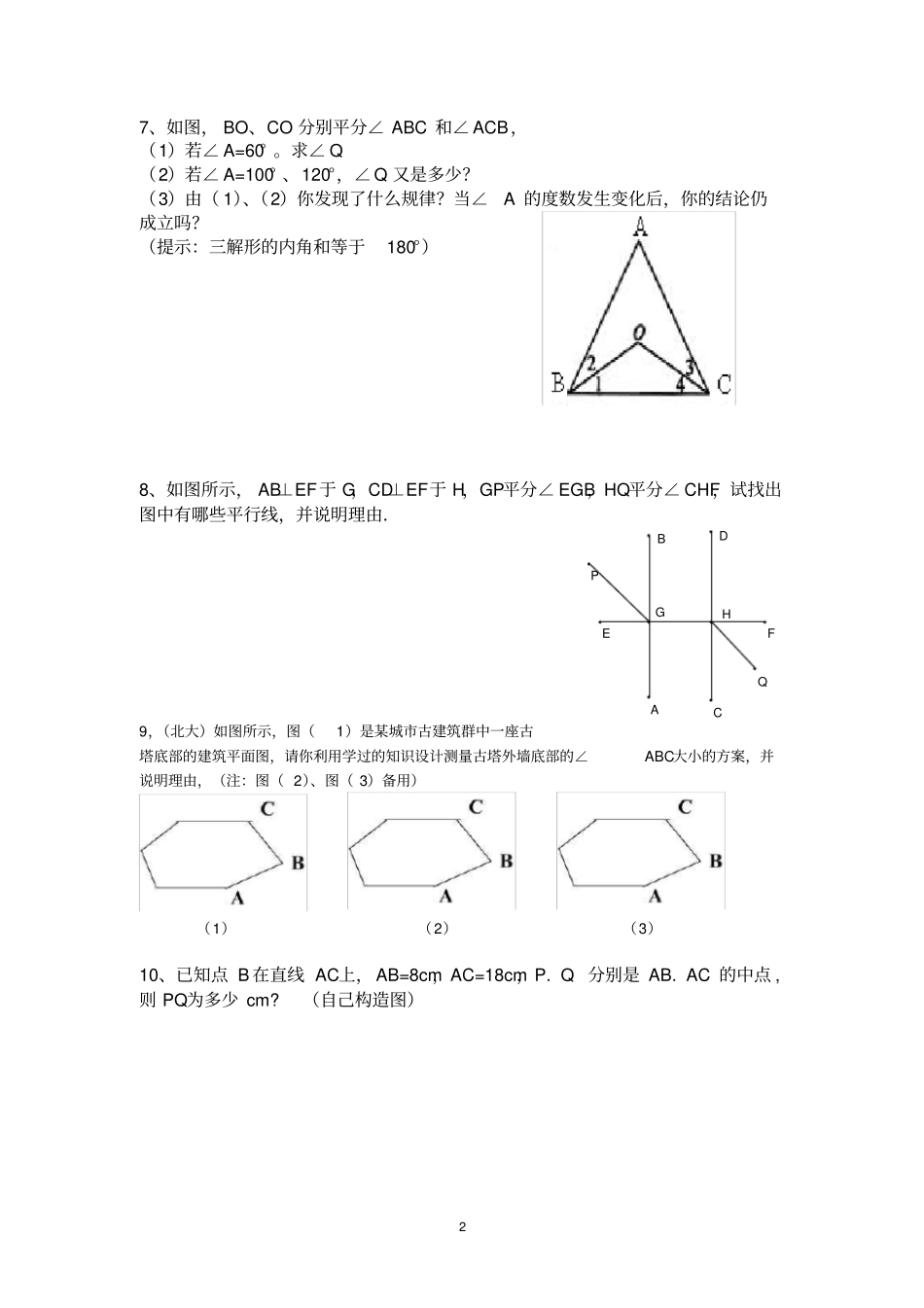
1七年级数学(下)培优竞赛试题1、已知直线AB、CD、EF相交于点O,∠1:∠3=3:1,∠2=20度,求∠DOE的度数。2、如图所示,O为直线AB上一点,∠AOC=13∠BOC,OC是∠AOD的平分线。①求∠COD的度数;②判断OD与AB的位置关系,并说明理由。3、如图,两直线AB、CD相交于点O,OE平分∠BOD,如果∠AOC:∠AOD=7:11,①求∠COE;②若OF⊥OE,∠AOC=70°,求∠COF。4、如图⑺,在直角ABC中,∠C=90°,DE⊥AC于E,交AB于D.①指出当BC、DE被AB所截时,∠3的同位角、内错角和同旁内角.②试说明∠1=∠2=∠3的理由.(提示:三角形内角和是1800)5、如图是一个3×3的正方形,则图中∠1+∠2+∠3+⋯+∠9=。6,(安徽中考)如图,已知AB∥DE,∠ABC=800,∠CDE=1400,则∠BCD=.321OFEDCBAODCBAABCDOEF63219875427、如图,BO、CO分别平分∠ABC和∠ACB,(1)若∠A=60°。求∠Q(2)若∠A=100°、120°,∠Q又是多少?(3)由(1)、(2)你发现了什么规律?当∠A的度数发生变化后,你的结论仍成立吗?(提示:三解形的内角和等于180°)8、如图所示,AB⊥EF于G,CD⊥EF于H,GP平分∠EGB,HQ平分∠CHF,试找出图中有哪些平行线,并说明理由.9,(北大)如图所示,图(1)是某城市古建筑群中一座古塔底部的建筑平面图,请你利用学过的知识设计测量古塔外墙底部的∠ABC大小的方案,并说明理由,(注:图(2)、图(3)备用)(1)(2)(3)10、已知点B在直线AC上,AB=8cm,AC=18cm,P.Q分别是AB.AC的中点,则PQ为多少cm?(自己构造图)ABCDEFGHPQ311、如图,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,∠DEC=90°,证明:AD∥BC12、如图,已知AB∥CD,∠1与∠D、∠B之间存在怎样的数量关系?13,如图,已知∠1+∠2=1800,∠3=∠B,试判断∠AED与∠ACB的大小关系。并对结论进行证明。14、已知,如图,CD⊥AB,GF⊥AB,∠B=∠ADE,试说明∠1=∠2.15,如图,平行直线AB、CD与相交直线EF,GH相交,则图中的同旁内角共有()A,4对B,8对C,12对D、16对(15题)(16题)(17题)16,如图,已知直线AB∥CD,则∠1+∠3--∠2的度数是()A,900B,1200C,1500D,1800,ABECD1F21GEDCBA417,如图、已知AB∥CD,∠1=1000,∠2=1200,则∠a=.18,如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐的角是1200,第二次拐的角是1500,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是()A,1200B,1300C,1400D,150019.如图3,锐角△ABC中,AD和CE分别是BC和AB边上的高,若AD与CE所夹的锐角是58°,则∠BAC+∠BCA的大小是。20,(北大)在同一平面内,3条直线两两相交,最多有3个交点,那么4条直线两两相交,最多有()个交点,8条直线两两相交,最多有()个交点。21,观察如图所示中的各图,寻找对顶角(不含平角):(1)如图a,图中共有___对对顶角;(2)如图b,图中共有___对对顶角;(3)如图c,图中共有___对对顶角.(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成多少对对顶角?(5)若有2008条直线相交于一点,则可形成多少对对顶角?22.如图(1),点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点。(1)求线段MN的长;(2)若C为线段AB上任一点,满足AC+CB=acm,其它条件不变,你能猜想MN的长度吗?并说明理由。(3)如图(2)若C在线段AB的延长线上,且满足ACBC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由。ABCMNABCDOabcAABBCCDDOOEFGH图a图b图c图(1)AB图(2)ABCDE58°图3