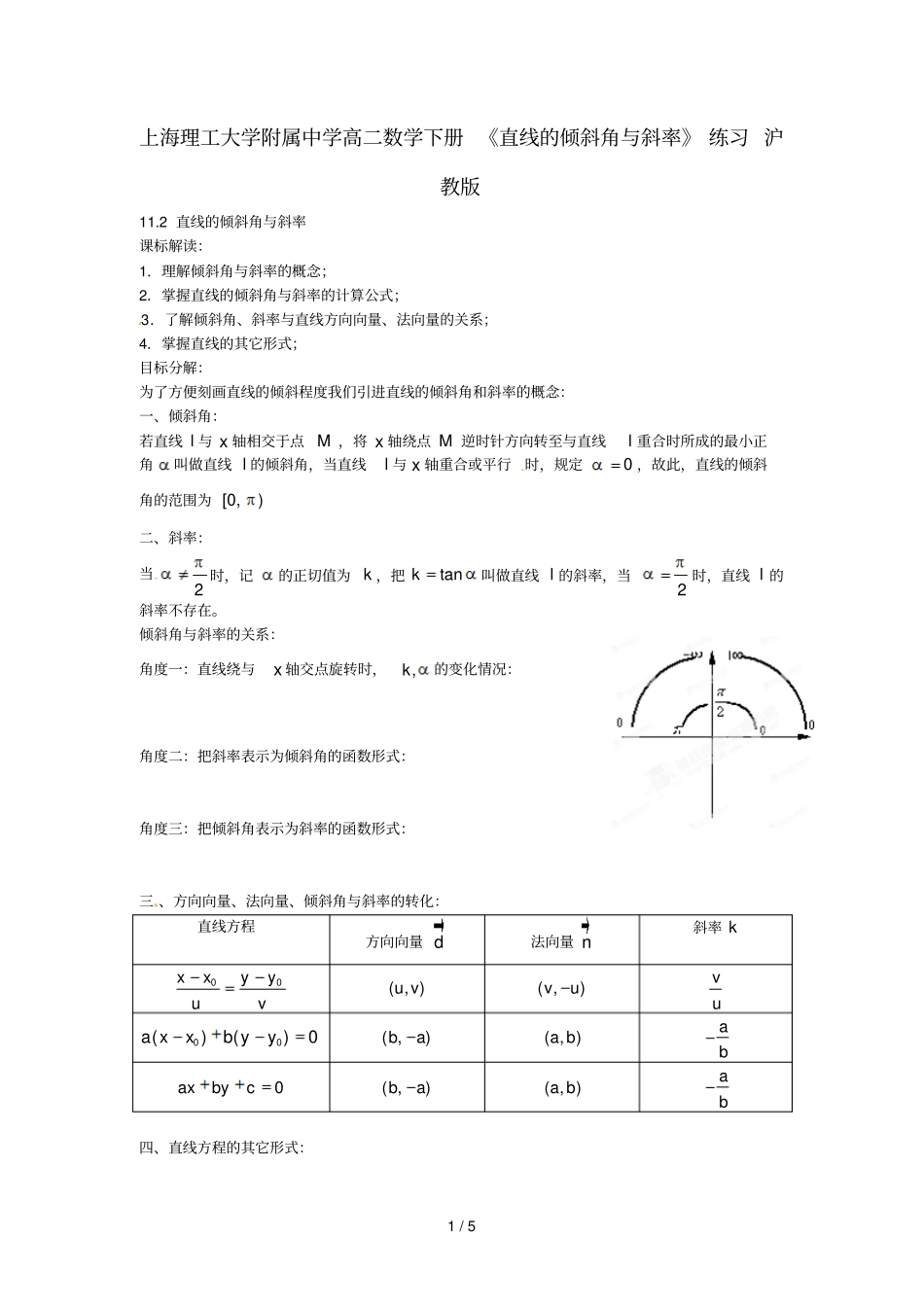
1/5上海理工大学附属中学高二数学下册《直线的倾斜角与斜率》练习沪教版11.2直线的倾斜角与斜率课标解读:1.理解倾斜角与斜率的概念;2.掌握直线的倾斜角与斜率的计算公式;3.了解倾斜角、斜率与直线方向向量、法向量的关系;4.掌握直线的其它形式;目标分解:为了方便刻画直线的倾斜程度我们引进直线的倾斜角和斜率的概念:一、倾斜角:若直线l与x轴相交于点M,将x轴绕点M逆时针方向转至与直线l重合时所成的最小正角叫做直线l的倾斜角,当直线l与x轴重合或平行时,规定0,故此,直线的倾斜角的范围为[0,)二、斜率:当2时,记的正切值为k,把tank叫做直线l的斜率,当2时,直线l的斜率不存在。倾斜角与斜率的关系:角度一:直线绕与x轴交点旋转时,,k的变化情况:角度二:把斜率表示为倾斜角的函数形式:角度三:把倾斜角表示为斜率的函数形式:三、方向向量、法向量、倾斜角与斜率的转化:直线方程方向向量d法向量n斜率k00xxyyuv(,)uv(,)vuvu00()()0axxbyy(,)ba(,)abab0axbyc(,)ba(,)abab四、直线方程的其它形式:2/5(1)斜截式:ykxb;(2)点斜式:00()yykxx;(3)截距式:1xyab注意:上述直线方程形式有的不能表示所有的平面内的直线方程,它们的先天不足需要引起我们的重视。例1.已知直线l上两点,AB,求直线l的倾斜角和斜率k(1)(1,3),(5,1)AB;(2)(1,2),(1,1)AB;(3)(0,5),(1,5)AB例2.直线l过点(,3),(1,1)AaB,求直线l的斜率和倾斜角;例3.(1)已知直线斜率2k,求倾斜角及一个方向向量;(2)已知直线l的一个方向向量为(3,3)d,求直线l的倾斜角和斜率;例4.求直线sin1yx的倾斜角的范围;例5.已知(1,5),(3,2)MN,若直线l的倾斜角是直线MN的倾斜角的一半,求直线l的斜率;例6.已知(3,1),(5,1),(2,31)PMN,直线l过点P且与线段MN相交(1)求直线l斜率k的取值范围;(2)直线l的倾斜角的取值范围;练习:已知(2,3),(3,2),MN直线l经过点(1,1)P,且与线段MN相交,求直线l的斜3/5率k及倾斜角的取值范围;例7.已知直线l的方程:(2)(12)430axaya(aR)(1)求证:不论a为何值,直线l恒过定点;(2)记上述定点为P,若lOP(O为原点),求实数a的值;例8.ABCD为平行四边形,其中三个顶点的坐标依次为:(2,3),(2,4),(6,1)ABC,求直线AD与直线CD的方程;例9.求经过点(3,5)P,且在两坐标轴上的截距相等的直线方程;例10.已知直线l过点(2,1)P,且与x轴,y轴的正半轴分别交于,MN两点,求使得MONS最小时的直线方程。4/5一页纸训练:1.已知点(2,3),(1,5)AB,则直线AB的倾斜角为______________;2.已知直线经过一点(6,4)A,斜率为43,则直线的一般式方程为_______________;3.直线l的倾斜角为6,l上有两点(1,3),(4,)ABy,则_______________y;4.一直线经过(2,3)P倾斜角是直线12yx的倾斜角的两倍,则该直线方程为_________;5.已知直线l的斜率3(,2)(,)4k,则直线l的倾斜角的范围是___________;6.直线l的斜率k满足[1,2)k,则直线l的倾斜角的取值范围是______________;7.直线l的倾斜角是060,当直线l绕着直线上一点逆时针旋转090,则直线l的斜率k的变化范围是____________;8.已知两点(3,3),(4,5)AB,直线:1lykx与线段AB有公共点,则直线l的倾斜角的取值范围是_____________;9.已知点(3,1)M,点N与点M的连线的倾斜角为3arctan4,若3MN,则N坐标为:________;10.若直线l满足如下条件,分别求出其方程:(1)斜率为34,与坐标轴围成的面积为6;(2)经过两点(1,0),(,1)ABm;(3)将直线l绕其上一点P沿顺时针旋转角,所得直线方程是20xy,若继续旋转2,所得的直线方程为210xy;(4)过点(,0)(0)aa且割第二象限得到一个面积为S的三角形区域;11.已知直线:120()lkxykkR(1)证明直线恒过一定点;5/5(2)若直线l分别于x轴的负半轴交于点A,与y轴的正半轴交于点B,求AOBS的最小值,及此时直线l的方程;(3)若直线l不经过第四象限,求k的取值范围。