考试资料.统计学三大分布与正态分布的关系[1]张柏林41060045理实1002班摘要:本文首先将介绍X2分布,t分布,F分布和正态分布的定义及基本性质,然后用理论说明X2分布,t分布,F分布与正态分布的关系,并且利用数学软件MATLAB来验证之.1.三大分布函数[2]匸1X2分布X2(n)分布是一种连续型随机变量的概率分布。这个分布是由别奈梅(Benayme)、赫尔默特(Helmert)、皮尔逊分别于1858年、1876年、1900年所发现,它是由正态分布派生出来的,主要用于列联表检验。定义:若随机变量X,X,相互独立,且都来自正态总体N(O,1),则称12n统计量X2为服从自由度为n的X2分布,记为X2~X2(n).12nX2分布的概率密度函数为nxx2_1e-2其中伽玛函数r(x)=于e-ttx-idt,x>0,X2分布的密度函数图形是一个只取非负值0的偏态分布,如下图.12f(x;考试资料.:E(%2(n))二n,D(咒2(n))二2n;若X=%2(n),X=%2(n),X,X相互独立,则X+X〜%2(n+n);1122121212n时,%2()T正态分布;性质4:设%2-%2(n),对给定的实数aa(0
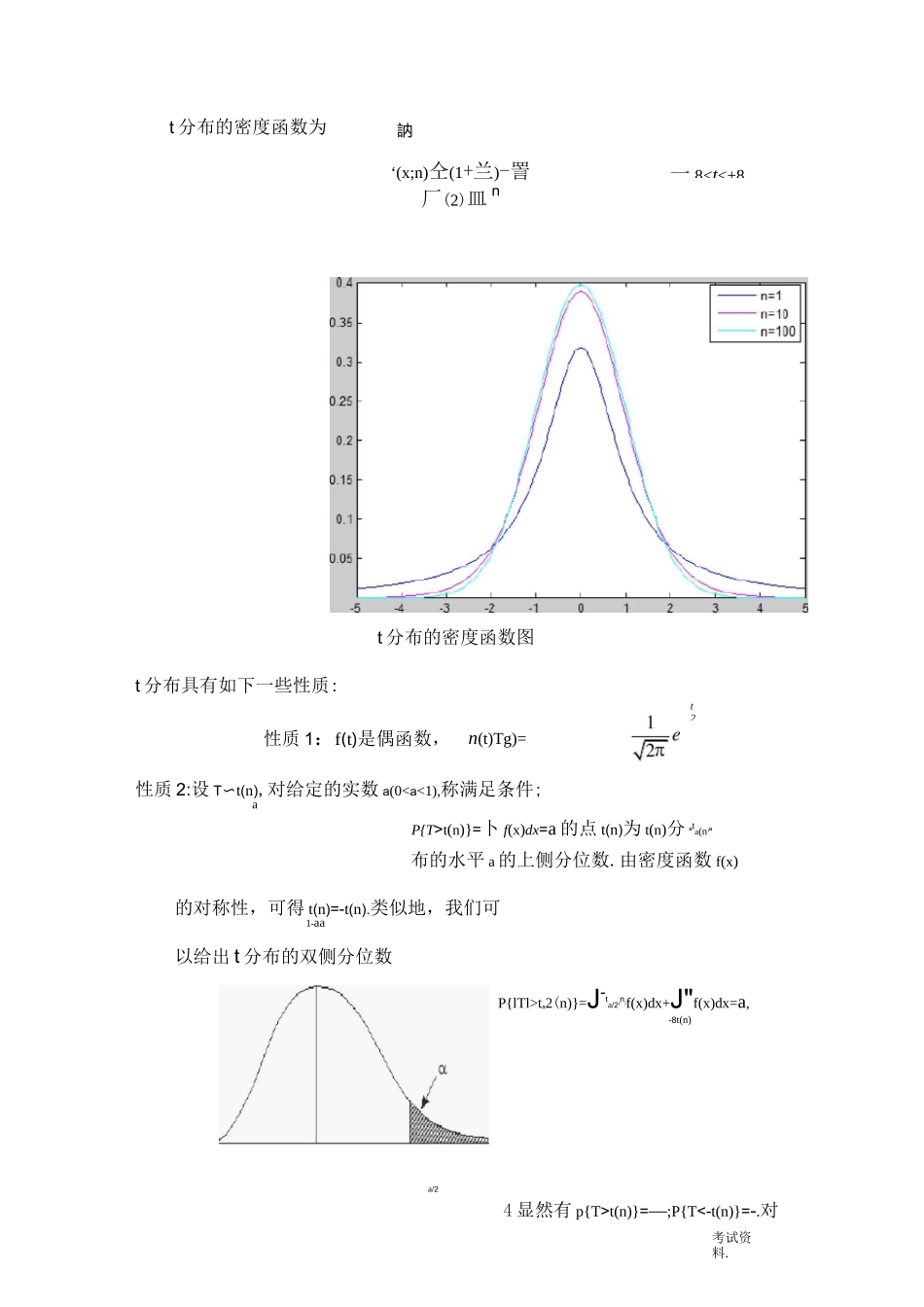
%2(n)}=f(x)dx=aa%a(n)的点%2(n)为%2(n)分布的水平a的上侧a分位数.简称为上侧a分位数.对不同的a与n,分位数的值已经编制成表供查分布的上a分位数分布也称为学生分布,是由英国统计学家戈赛特在1908年“student”的笔名首次发表的,这个分布在数理统计中也占有重要的位置定义:设X〜N(O,),〜%2(),X,Y相互独立,则称统计量T=「亠服Y/n从自由度为n的t分布,记为T〜t(n).卡方分布具有如下基本性质:一8t(n)}=卜f(x)dx=a的点t(n)为t(n)分ata(n)a布的水平a的上侧分位数.由密度函数f(x)的对称性,可得t(n)=-t(n).类似地,我们可1-aa以给出t分布的双侧分位数P{lTl>ta2(n)}=J-ta/2(n)f(x)dx+J"f(x)dx=a,-8t(n)a/24显然有p{T>t(n)}=—;P{T<-t(n)}=-.对n(t)Tg)=nt2訥考试资料.a/22a/22不同的«与n,t分布的双侧分位数可从附表查得.t分布的上«分位数1.3F分布F分布是随机变量的另一种重要的小样本分布,应用也相当广泛.它可用来检验两个总体的方差是否相等,多个总体的均值是否相等.F分布还是方差分析和正交设计的理论基础.定义:设X〜咒2(n),Y〜X2(m),X,Y相互独立,令则称统计量F二仏服Y/m从为第一自由度为n,第二自由度为m的F分布.F分布的密度函数图F分布具有如下一些性质:性质1:若F〜F(n,m),则1/F〜F(m,n).5性质2:若X-1(n),则X2~F(1,n);0尽個厂1,迪考试资料.f(x)=(x-M)2202,-g0)为常数,则称X服从参性质3:设F〜F(n,m),对给定的实数d(0F(n,m)}=f(x)dx=aF(n,m)a的点F(n,m)为F(n,m)分布的水平a的上侧分位数.aF分布的上a分位数F分布的上侧分位数的可自附表查得.性质4:F(m,n)=1.此式常常用来求F分布表中没有列出的某些上侧aF(n,m)1-a分位数.1.4正态分布正态分布是数理统计中的一种重要的理论分布,是许多统计方法的理论基础.高斯(Gauss)在研究误差理论时首先用正态分布来刻画误差的分布,所以正态分布又称为高斯分布.正态分布有两个参数,卩和6决定了正态分布的位置和形态.为了应用方便,常将一般的正态变量X通过u变换转化成标准正态变量u,以使原来各种形态的正态分布都转换为卩=0,。=1的标准正态分布N(,).正态分布的密度函数和分布函数若连续型随机变量X具有概率密度f(x)为为M,o的正态分布,记为X〜N(M,o2).考试资料.正态分布的密度函数图特征1:正态曲线(normalcurve)在横轴上方均数处最高;特征2:正态分布以均数为中心,左右对称;特征3:正态分布有两个参数,即均数卩和标准差a.卩是位置参数,a固定不变时,卩越大,曲线沿横轴越向右移动;反之,卩越小,则曲线沿横轴越向左移动.a是形状参数,当卩固定不变时,a越大,曲线越平阔;a越小,曲线越尖峭.通常用Ng,a2)表示均数为卩,方差为a2的正态分布.用N(,)表示标准正态分布.特征4:正态曲线下面积的分布有一定规律。实际工作中,常需要了解正态曲线下横轴上某一区间的面积占总面积的百分数,以便估计...