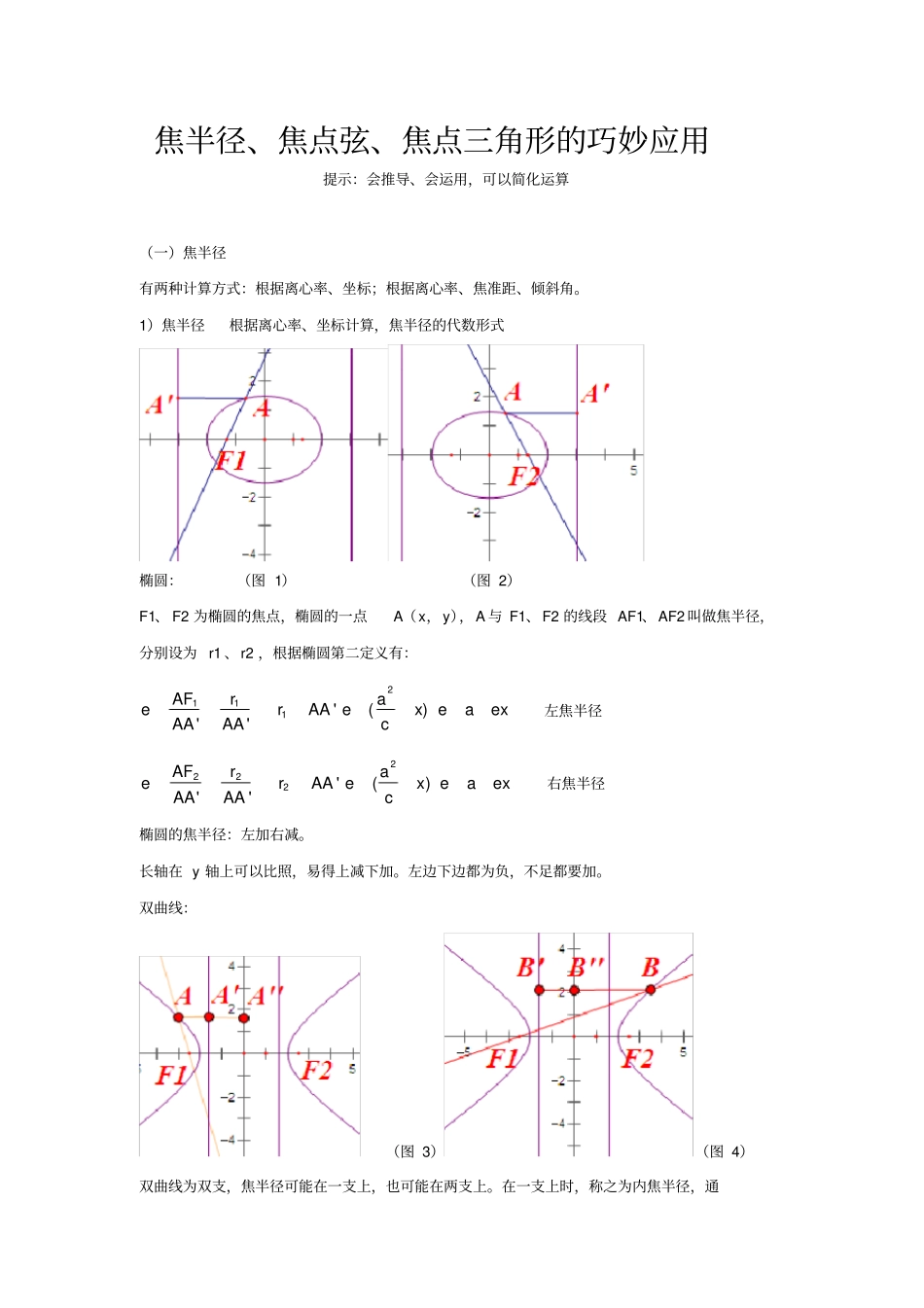
焦半径、焦点弦、焦点三角形的巧妙应用提示:会推导、会运用,可以简化运算(一)焦半径有两种计算方式:根据离心率、坐标;根据离心率、焦准距、倾斜角。1)焦半径根据离心率、坐标计算,焦半径的代数形式椭圆:(图1)(图2)F1、F2为椭圆的焦点,椭圆的一点A(x,y),A与F1、F2的线段AF1、AF2叫做焦半径,分别设为r1、r2,根据椭圆第二定义有:2111'()''AFraerAAexeaexAAAAc左焦半径2222'()''AFraerAAexeaexAAAAc右焦半径椭圆的焦半径:左加右减。长轴在y轴上可以比照,易得上减下加。左边下边都为负,不足都要加。双曲线:(图3)(图4)双曲线为双支,焦半径可能在一支上,也可能在两支上。在一支上时,称之为内焦半径,通常也叫焦半径。在两支上叫外焦半径。以焦点在左支上为例,推导左焦半径公式。设内焦半径AF1为r1,根据双曲线第二定义有:2111'(''''')()''FAraerAAeAAAAexeaexAAAAc同理,右支2211'()''FAraerAAexeaexAAAAc双曲线焦半径,与椭圆有两点相反,左减右加,半长轴取反。实轴在y轴上,可以比照,易得上加下减。联想特征:左边下边都为负,要减一起减。可以从图形上理解,双曲线的左半支相当于抛物线的右半支。以左焦点为起点的外焦半径,根据双曲线第二定义有:2122'(""')()''FBraerBBeBBBBexeaexBBBBc同理,以右焦点为起点的外焦半径公式:2222'()''FBraerBBexeaexBBBBc双曲线外焦半径,与椭圆相同。不作要求,高考中未见。抛物线:抛物线22(0)ypxp,C(x,y)为抛物线上的一点,焦半径|CF|=|x|+2p。例1(2000年高考(理工)22题)已知梯形ABCD中,|AB|=2|CD|,点E分有向线段ACuuur所成的比为,双曲线过C、D、E三点,且以A、B为焦点。当2334,求双曲线的离心率的取值范围。解析:这是一道高考压轴题,难度较大。建立坐标系,给出A、B坐标,由|AB|=2|CD|和对称性可知C的坐标为(,2ch),h为梯形的高。由定比分点公式可求出E的坐标,而E、C都在双曲线上,代入双曲线方程。这是常规处理方式,很费事。常规解法见。这里用焦半径概念求解。根据向量知识或定比分点公式,先求出E、C的横坐标,再求焦半径AE、AC,这样,只用处理和c的关系,关系简单纯粹。AE=Eexa,AC=Cexa,EC=AC-AE=()2CEexxa,()2ECEexaAEECexxa将(2)212(1)Ecccx,2Ccx代入上式,则(2)2(1)(2)[]222(1)ceaccea即222(2)12132(1)21(2)11[]222(1)eee。再由2334,得到3341,372101,即710e。2)焦半径根据离心率、焦准距、倾斜角计算,焦半径的统一公式长焦半径r=1cosepe,短焦半径r=1cosepe。根据图象判断,如椭圆的左上支,椭圆的右下支,就是长焦半径,无需记忆。同样,双曲线、抛物线也是根据图象判断长短。外焦半径,只有双曲线才有,比较复杂,且高考中,暂未发现此类题目,只简单介绍。(图5)(图6)内外焦半径推导如下:椭圆的左半边、双曲线右支、开口向右的抛物线的内分焦半径推导:111cos1cosAFAFAFAFepeAFAAAAAMMApAFe(*)椭圆的右半边、双曲线左支、开口向左的抛物线的内分焦半径推导:111cos1cosBFBFBFBFepeBFBBBBNBNBpBFeBF也可根据AF直接写出,为线段与正方向的夹角,这时为+π。外分焦半径,仅双曲线拥有,这里以从左焦点伸向右支为例(不作要求):11coscos1AFAFAFepeAFAAAMAMAFpeP叫焦准距,p=2bc(椭圆、双曲线)。例2(2012江苏高考19题)如图,在平面直角坐标系xOy中,椭圆22221(0)xyabab的左右焦点分别为F1(-c,0),F2(c,0)。已知(1,e)和(e,32)都在椭圆上,其中e为椭圆的离心率。(1)求椭圆的方程;(2)设A,B是椭圆上位于X轴上方的两点,且直线AF1与直线BF2平行,AF2、BF1交于点P。(i)若AF1-BF2=62,求直线AF1的斜率;(ii)求证PF1+PF2是定值。解析:这道题压轴题,很难,据闻得分率很低。(1)代入两已知点易求得a、b的值;(2)的(i)按通法应设出AF1、BF2方程,分别与椭圆方程联立,得出AF1、BF2的长。可设x=my-1或x=my+1。(ii)一看就知可能要用平面几何的平行线性质。显然用焦半径的统一公式或者焦半径的代数形式能简化运算。解:(1)将两已知点代入椭圆方程有22222222222222242111123314411eababaababeababab所以椭圆方程是2212xy。(2)解一:焦半径的...