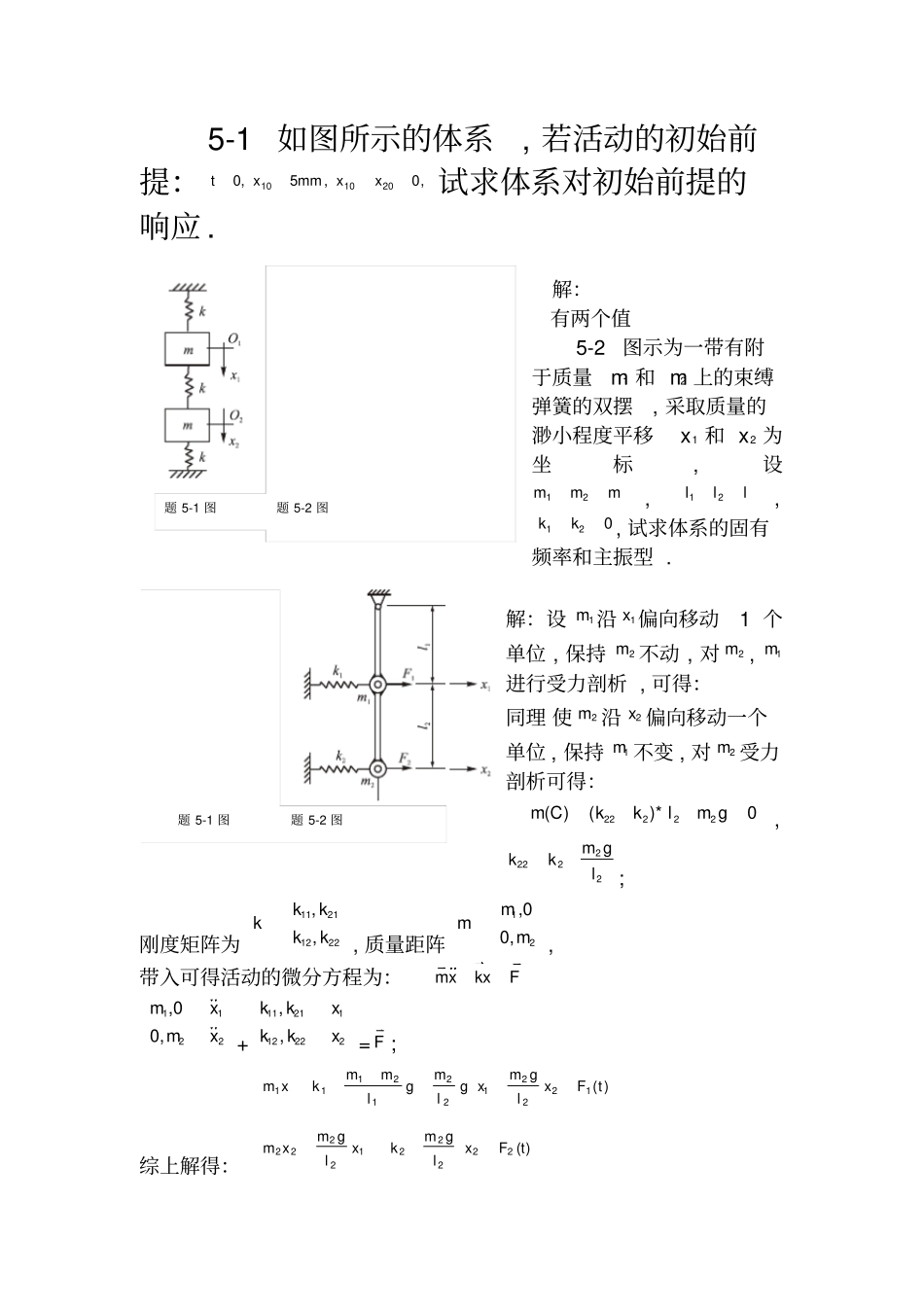
5-1如图所示的体系,若活动的初始前提:,0,mm5,0201010xxxt试求体系对初始前提的响应.解:有两个值5-2图示为一带有附于质量m1和m2上的束缚弹簧的双摆,采取质量的渺小程度平移x1和x2为坐标,设mmm21,lll21,021kk,试求体系的固有频率和主振型.解:设1m沿1x偏向移动1个单位,保持2m不动,对2m,1m进行受力剖析,可得:同理使2m沿2x偏向移动一个单位,保持1m不变,对2m受力剖析可得:22222()()*0mCkklmg,22222mgkkl;刚度矩阵为11211222,,kkkkk,质量距阵12,00,mmm,带入可得活动的微分方程为:mxkxF12,00,mm12xx+11211222,,kkkk12xx=F;综上解得:)()(2222212222122212212111tFxlgmkxlgmxmtFxlgmxglmglmmkxm题5-1图题5-2图题5-1图题5-2图应用刚度影响系数法求刚度矩阵k.设0,121xx,分离画出1m与2m的受力争,并施加二物块力2111,kk,列均衡方程,对1m:0X,0sinsin1221111kTTk0Y,0coscos12211gmTT对2m:0X,0sin2221Tk0Y,0cos222gmT设1,021xx,分离画出1m与2m的受力争,并施加二物块力2212,kk,列均衡方程,对1m:0X,0sin212Tk0Y,0cos121gmTT对2m:0X,0sin2222Tkk0Y,0cos22gmT由,1111tansinl,2221tansinl,1coscos21,1cos,21tansinl,解得,22121111)(lgmlgmmkk,2221lgmk,2212lgmk,22222lgmkk得感化力方程为由方程得到体系的刚度矩阵为K=lmglmglmglmg3体系的质量矩阵为M=mm00由频率方程02MKp,得睁开为0242222224gmgmlplmp,解出频率为由特点矩阵MKB2p的陪同矩阵的第一列,lmgmplmgadj2)1(B并分离代入二频率值,得到二阶振型为1211312mglVmgpml,2211312mglVmgpml1211)1(A,1211)1(A体系的主振型矩阵为5-3图示的扭振体系由无质量的轴和两个圆盘构成,已知轴段的扭转刚度为kq1及kq2,圆盘的迁移转变惯量为I1.I2,并受到扭矩M1.M2的感化,试写出体系活动的微分方程,并求体系的固有频率和主振型.题5-3图解:取12,为广义坐标,它们分离为M1.M2的转角.当1=1,2=0时,1121,kk分离暗示保持体系该地位均衡,应加在M1.M2的力偶矩,由刚体的均衡前提得当1=0,2=1时,1121,kk分离暗示保持体系该地位均衡,应加在M1.M2的力偶矩,由刚体的均衡前提得对12,取随意率性值时,依据达朗贝尔道理,可得体系的微分方程为即5-4图示悬臂梁的质量不计,梁的抗弯刚度为EI,设mmm21,试写出体系活动的微分方程,并求体系的固有频率和主振型.题5-4图解:取为12,xx广义坐标,依据柔度影响系数的界说,11暗示在1m处施加单位力(沿1x偏向)在1m处产生的位移.按材料力学的挠度公式,则有22暗示在2m处施加单位力(沿2x偏向)在2m处产生的位移.有1221暗示在2m处施加单位力在1m处产生的位移等于在1m处施加单位力在2m处产生的位移.有体系的位移方程即有所求微分方程为解:体系的质量矩阵M=mm00.起首仅在质量m1处施加竖直单位力Q=1,则m1产生的位移是:δ11;m2产生的位移是:δ21.画出m1的受力争,如图(1).0x时,'v=0,所以1c=0;v,所以1d=0.2lx时,31124lEI;认为异常小,所以有sin'v,再在2m上施加单位力,则1m处产生的位移为12,2m处产生的位移为22.画出2m的受力争如图(2).0x时,'0v,所以20c;0v,所以20d.2lx时,312545lEIxl时,3221648lEI于是可以写出柔度矩阵体系的特点矩阵令348mlEI,21p,则有25516L频率方程,0L得求出各根117.620.4于是得到固有频率131.65EIpml2310.95EIpml为求体系的主振型,先求adjL16552adjL将1,2分离代入第一列,则各阶主振型为5-5如图所示,拉紧的无质量弦上附着两个质量m1与m2,假定质量作横向微振动时弦中拉力FT不变,设mmm21,试写出体系活动的微分方程,并求体系的固有频率和主振型.5-5图解:在竖直偏向以m1为坐标原点树立y坐标(正偏向竖直向下).令m1有单位位移1y=1,而2m保持不动,1112kk分离暗示保持体系在该地位均衡,应在12mm施加的力,由刚体12mm的均衡前提得11212/,/ttkFlkFl.再令2m有单位们移2y=1,同理可得1222/,2/ttkFlkFl.是以,可得到刚度矩阵111221222///2/ttttFlFlkkKFlFlkk可写出体系活动的微分方程为..0MxKx,整顿后得解:令1x=1,2x=011k=2TFsin=2TFtan=2TF1l=2TFl(0)21TFkl令211,0xx同理得222TFkl12TFkl图5——5所以体系活动的微分方程为:解:体系的质量矩阵M=mm00.起首仅在质量m1处施加竖直单位力Q=1,则m1产生的位移是:δ11;m2产生的位移是:δ21.画出m...