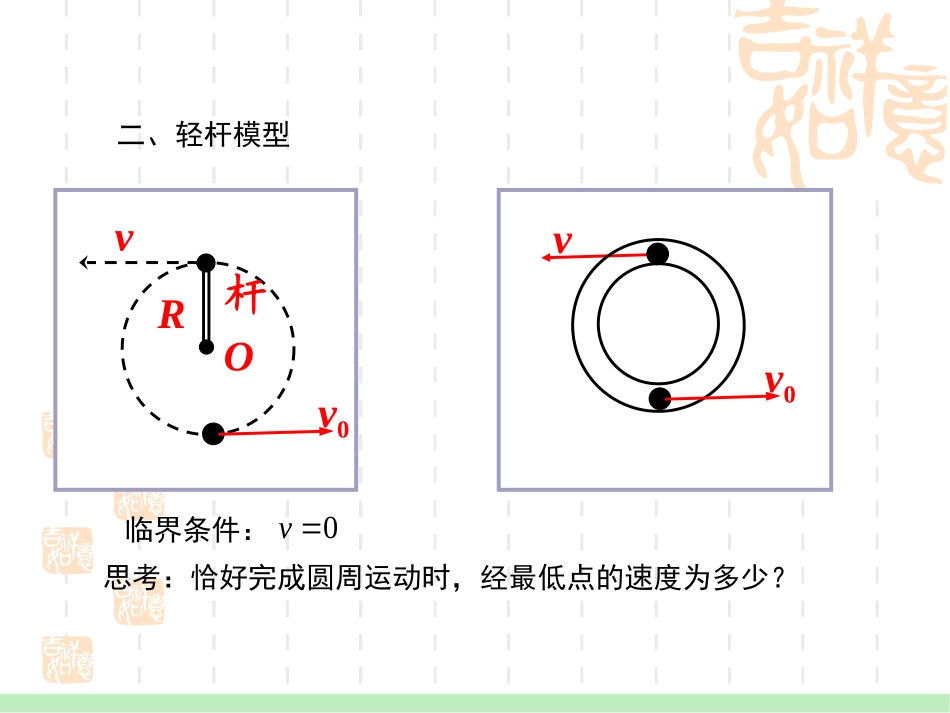
第三节圆周运动一、轻绳模型竖直平面内的圆周运动Rvv0临界条件:grv思考:恰好完成圆周运动时,经最低点的速度为多少?ROv绳v0二、轻杆模型vv0ROv杆v0临界条件:0v思考:恰好完成圆周运动时,经最低点的速度为多少?例题一.如图4-3-9所示,光滑圆管形轨道AB部分平直,BC部分是处于竖直平面内半径为R的半圆,圆管截面半径r≪R,有一质量为m、半径比r略小的光滑小球以水平初速度射入圆管..(1)若要小球能从C端出来,vc应为多大?(2)在小球从C端出来瞬间,对管壁压力有哪几种典型情况?vc各应满足什么条件?图4-3-9设小球经最高点时管壁对球的弹力为FN,速度为v,试作出FN-v2的图线解:取竖直向下为正方向增大减小②小球过最高点时,所受弹力情况:A.小球到达最高点的速度v=0,此时轻杆或管状轨道对小球的弹力N=mg.B.当小球的实际速度v>gR时,轻杆对小球产生竖直向下的拉力,管状轨道对小球产生竖直向下的压力,因此FN=mv2R-mg,所以弹力的大小随v的增大而_____.C.当00所以入射速度v0>2gR.(2)小球从C端出来瞬间,对管壁压力可以有三种典型情况:①刚好对管壁无压力,此时重力恰好充当向心力,由圆周运动知识得mg=mv2CR由机械能守恒定律:12mv20=mg·2R+12mv2C联立解得v0=5gR②对下管壁有压力,此时应有mg>mv2CR相应的入射速度v0应满足2gR<v0<5gR③对上管壁有压力,此时应有mg<mv2CR相应的入射速度v0应满足v0>5gR.2.圆周运动的临界问题(1)轻绳模型:没有物体支撑的小球,在竖直平面内做圆周运动过最高点,如图4-3-3所示:图4-3-3图4-3-4①由牛顿运动定律知mg=mv2R,得小球过圆周轨道最高点的临界速度为v0=5gR.此时v=gR,它是小球通过圆周最高点的最小速度.(2)轻杆模型:有物体支撑的小球在竖直平面内做圆周运动的情况,如图4-3-4所示.①由于轻杆或管状轨道对小球有支撑作用,不存在“掉下②当mggR,小球能过圆周的最高点,此时绳和轨道分别对小球产生拉力和压力.③当mg>mv2R,即vgR时,轻杆对小球产生竖直向下的拉力,管状轨道对小球产生竖直向下的压力,因此FN=mv2R-mg,所以弹力的大小随v的增大而_____.C.当0