数学七年级下华师大版913三角形的三边关系课件(1)VIP免费

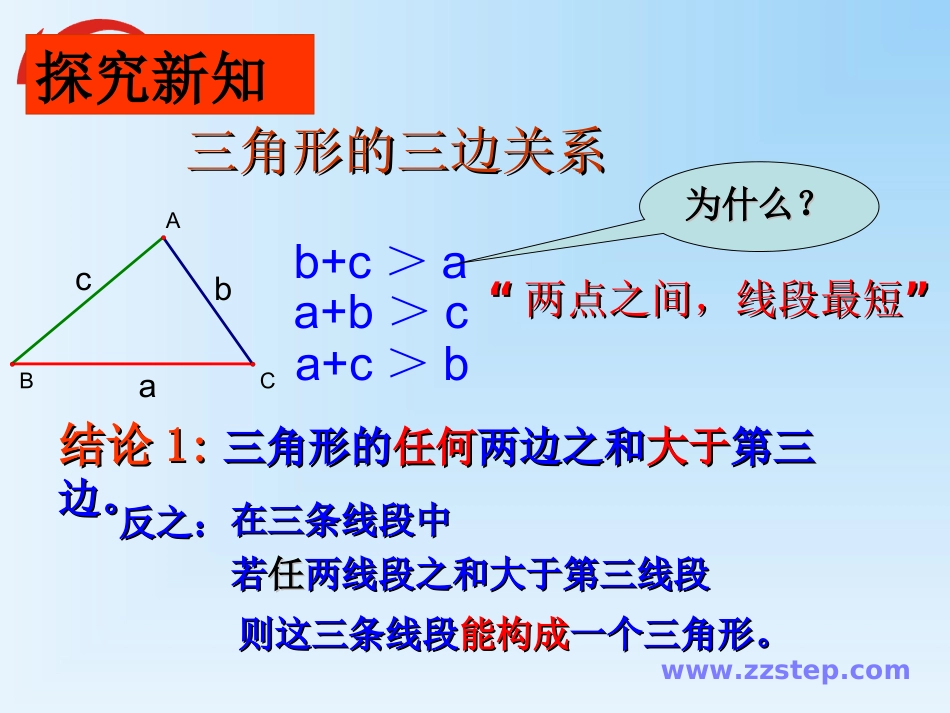
www.zzstep.comwww.zzstep.com1.画一个三角形，使它的三条边长分别为4cm、3cm、2.5cm.复习引入2.以下列长度的各组线段为边，能否画一个三角形.（1）5cm,4cm,3cm;（2）5cm,3cm,2cm;（3）5cm,2cm,2cm;www.zzstep.com三角形的三边关系三角形的三边关系““”两点之间，线段最短”两点之间，线段最短acbABCa+b＞cb+c＞aa+c＞b结论结论1:1:三角形的三角形的任何任何两边之和两边之和大于大于第三第三边。边。为什么？为什么？反之：反之：在三条线段中在三条线段中若若任任两线段之和大于第三线段两线段之和大于第三线段则这三条线段则这三条线段能构成能构成一个三角形。一个三角形。探究新知www.zzstep.com已知三角形两边已知三角形两边aa、、bb长为长为99、、55，，则第三边则第三边cc的取值范围的取值范围。。结论结论2:2:三角形的三角形的任何任何两边之差两边之差小于小于第三第三边。边。b+c＞aa+b＞ca+c＞ba-b＜cc-a＜bb-c＜a结论结论1:1:三角形的三角形的任何任何两边之和两边之和大于大于第三边。第三边。414cZ.x.x.Kwww.zzstep.com三角形三角形较短两边较短两边之和大于较长边。之和大于较长边。（3）3cm、8cm、5cm；（4）4cm、5cm、6cm.（1）15cm、10cm、7cm；（2）4cm、5cm、10cm；1.下列长度的各组线段能否组成一个三角形？(课本p821)2、判断：已知a+b>c，则以线段a、b、c为边能够成三角形。（）理解新知www.zzstep.com例1、在ΔABC中，AB=9，BC=2，并且AC为奇数，那么ΔABC的周长为。例2、如图，已知BM是ΔABC的中线，AB=6，BC=8，那么ΔMBC的周长与ΔABM的周长相差。MABC220灵活运用www.zzstep.com例3、己知⊿ABC是等腰三角形.(1)如果它的两条边的长分别为8cm和3cm,求它的周长;(2)如果它的周长为18cm,一条边的长为4cm,求它的腰长.(课本p821)解:(1)分两种情况:若8cm为底边长,若3cm为底边长,8cm,3cm,3cm不能构成三角形3cm,8cm,8cm可以构成三角形此时,周长为:3cm+8cm+8cm=19cm(2)分两种情况:若4cm为底边长,若4cm为腰长,腰长为:(18cm-4cm)÷2=7cm底边长为:18cm-4cm×2=10cm此时,4cm,4cm,10cm不能构成三角形.故腰长为:7cmwww.zzstep.com例4.已知ΔABC的两边AB=3cm，AC=8cm，(1)求第三边BC的取值范围；(2)若第三边BC的长为偶数，求BC的长；(3)若ΔABC为等腰三角形，求其周长(精编p6012):解(1)ACABBCACAB8383cmcmBCcmcm511cmBCcm2BC的长为偶数3ABC为等腰三角形6,8,10BCcmcmcm8BCACcmABCABBCAC的周长=88319()cm=Zx.xk