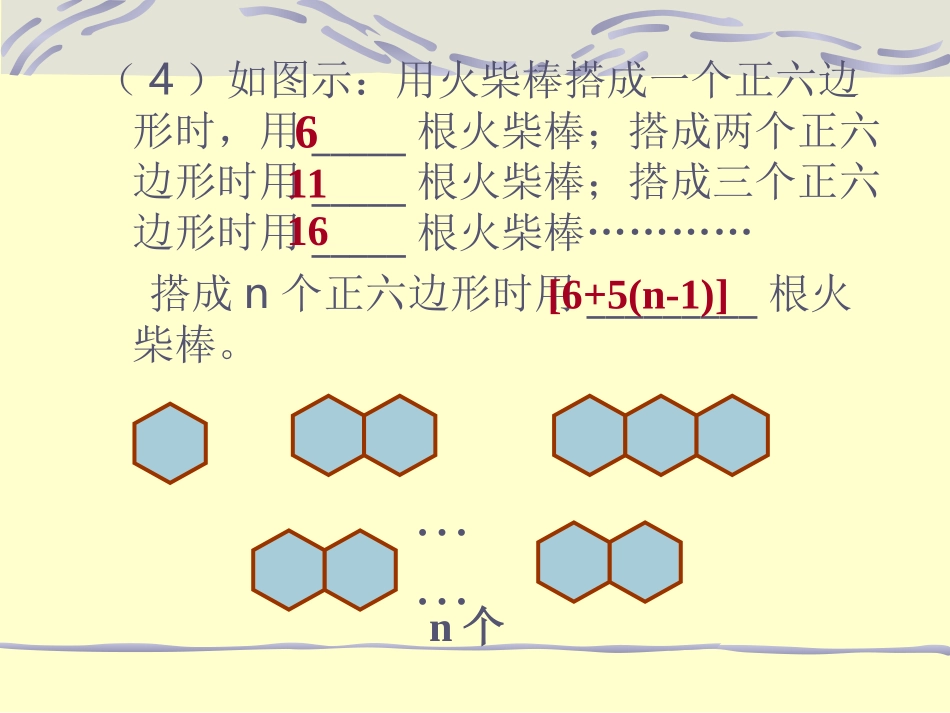
代数式一、复习引入:1、填空(1)边长为a厘米的正方形面积是_____平方厘米,体积是_______立方厘米。(2)小红第一次走3a千米,第二次走4a千米,两次共走________千米。(3)小彬第一天读书x页,第二天比第一天增加10%,第二天读书_________页。(3a+4a)(1+10%)x3aa²(4)如图示:用火柴棒搭成一个正六边形时,用_____根火柴棒;搭成两个正六边形时用_____根火柴棒;搭成三个正六边形时用_____根火柴棒…………搭成n个正六边形时用_________根火柴棒。……n个61116[6+5(n-1)]2、一辆汽车保持一定的速度行驶,每小时行驶60千米,这辆汽车行驶的路程与时间如下表:时间(时)12345…路程(千米)60120180240300…讨论:你能发现行驶的路程与时间存在什么规律吗?请用数学表达式表示出来。你知道你所用的数学表达式叫做什么吗?利用这一表达式你能很快算出10小时后汽车行驶的路程吗?二、新课讲授:1、代数式:像3a+4a,(1+10%)x,6+5(n-1),6,11,60t,s/t,等式子都是代数式。单独一个数或一个字母也是代数式。如:16,0,-2,a,n,x,2/3。注意:(1)代数式是用运算符,把数或字母连接起来的式子。(2)S=ab,a>b,这种等式,不等式都不是代数式。思考:代数式有哪些特点?,,32aa(3)代数式的书写格式:①数字与字母相乘,数字与括号相乘,可用“·”或省略乘号,并且把数字写在字母前面;字母与字母相乘,字母与括号相乘,括号与括号相乘可省略乘号;②数字与数字相乘,一般用“×”;③分数与字母相乘可省略乘号,带分数与字母相乘,一般把带分数化为假分数再与字母相乘;④有除号的,一般写成分数的形式。随堂练习:1、判断下列式子是否为代数式,并说明理由。(1)2x-y(2)a+b=c(3)x>4(4)-1(5)V=abc(6)2、说明下列各代数式书写的是否合理,并简要说明理由。xy213)1(cdab)2(3)3(y131x例1:列代数式,并求值。(1)某公园的门票价格是:成人票每张10元,学生票每张5元,一个旅游团有成人x人、学生y人,那么该旅游团应付多少门票费?把x=37,y=15代入代数式10x+5y,得10×37+5×15=445。因此,他们应付445元门票费。解:该旅游团应付的门票费是(10x+5y)元;(2)如果该旅游团有37个成人,15个学生,那么他们应付多少门票费?2、列代数式并求值列代数式:根据所给的语句,用代数式表示问题中的数量关系和变化规律;代数式求值:根据问题的要求,用具体数值代替代数式的字母,计算出的结果叫做代数的值。求值步骤:(1)代入;(2)计算想一想:代数式10x+5y还可以表示什么?例2:在某地,人们发现某种蟋蟀叫的次数与温度之间有如下的近似关系:用蟋蟀1分叫的次数除以7,然后再加上3,就近似地得到该地当时的温度(℃)。(1)用代数式表示该地当时的温度;(2)当蟋蟀1分叫的次数分别是80,100和120时,该地当时的温度约是多少?解:(1)用c表示蟋蟀1分叫的次数,则该地当时的温度为c/7+3.(2)把c=80,100和120分别代入c/7+3,得80/7+3=101/7≈14100/7+3=121/7≈17120/7+3=141/7≈20因此当蟋蟀1分叫的次数分别是80,100和120时,该地当时的温度大约分别是14℃,17℃和20℃例3:(1)张宇身高1.2米,在某时刻测得他影子的长度是2米。此时张宇的身高是他影长的多少倍?解:(1)1.2÷2=3/5,即此时张宇的身高是他影长的3/5倍。(2)如果用l表示物体的影长,那么如何用代数式表示此时此地物体的高度?(2)此时此地物体的高度为3l/5米。(3)该地某建筑物影长5.5米,此时它的高度是多少米?将=5.5代入3l/5,3/5×5.5=3.3(米)因此,建筑物此时的高度是3.3米。三、练习:1、填空(1)数a的1/8与这个数的和可以表示为_____.(2)一个两位数的个位数字是a,十位数字是b,请用代数式表示这个两位数;(3)如何用代数式表示一个三位数?2、(1)代数式(1+8%)x可以表示什么?(2)用具体数值代替(1+8%)x中的x,并解释所得代数式值的意义。3、一种树苗的高度h用表示,树苗生长的年数a用表示,测得的用关数据如下表(树苗原高度为100厘米):年数a1234……高度h(厘米)100+5100+10100+15100+20……写出用年数a表示高度h的代数式,并计算生长了6年的树苗的高度。四、小结:通过本节...