让教师智慧的教，引导学生聪明的学-数学VIP专享VIP免费

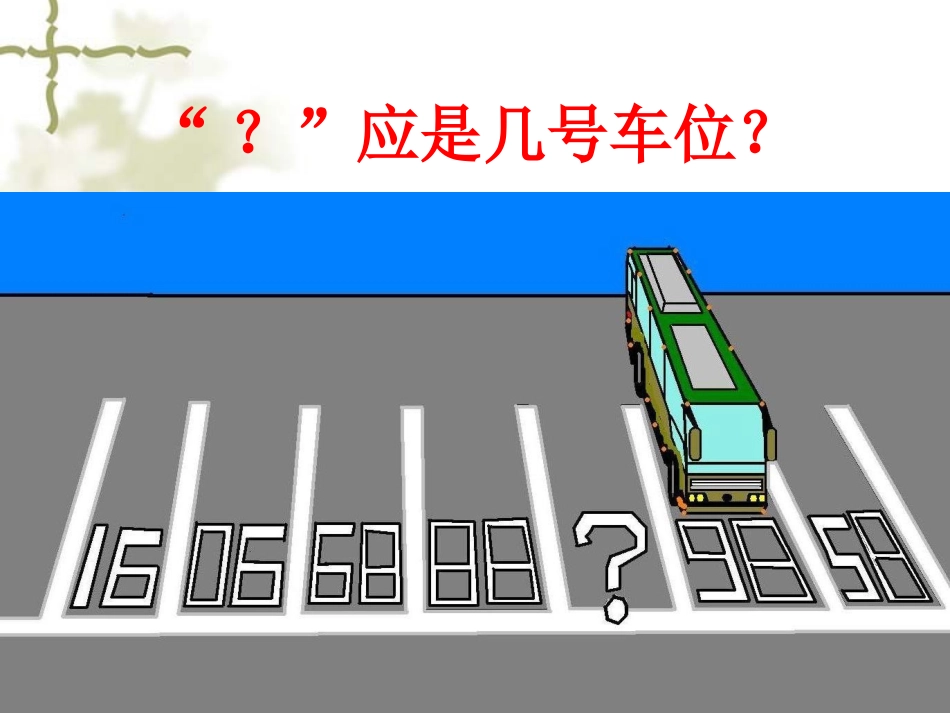
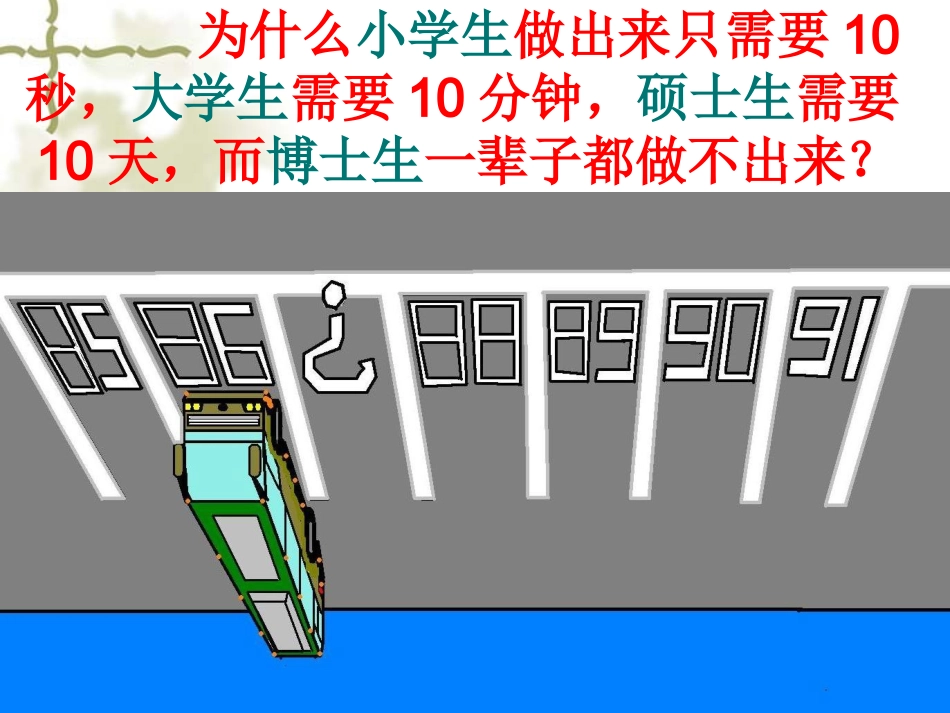
让教师智慧的教引导学生聪明的学“？”应是几号车位？为什么小学生做出来只需要10秒，大学生需要10分钟，硕士生需要10天，而博士生一辈子都做不出来？启迪建立以学习者为中心的教学观！《36天，我的美国教育之旅》-李希贵李希贵先生在美国哥伦比亚大学教育学院访学期间，和美国教育专家、教师一起分析课堂，碰撞教育智慧的经历。培训能给教师留下什么？2005年4月15日星期五今天的话题是从培训效果的评估开始的，就是我们怎么才能知道教师培训的效果。这个话题让我感到新鲜。在国内，各种各样面向中小学教师的培训正如火如荼地展开，可以说丰富多彩，也可以说名目繁多，但似乎很少有人关注培训的效果。大家热衷的是：我做了，我请来专家了，大家集中在一起听课了、鼓掌了，于是培训完成了……至于培训的效果如何，那又另当别论了。那么，真正让受训者学有所获呢？我们通常把培训效果更多地寄托在培训者身上，希望他们能口吐珠玑，妙手回春，教给给教师取之不尽、用之不竭的智慧，或者是一些攻能克、战能胜的法宝。真正好的培训则更多地关注为受训者多大程度上提供互动的机会，应该把大部分时间留给教师，让他们分组讨论，在碰撞中产生智慧，共同分享。分组怎么分？用智慧之泉浇灌聪明之苗的10个锦囊。1.深入知识的本质，渗透数学思想，升华数学思维。2.转变“三包”教学习惯，打造智慧课堂.3.智慧的课堂要做好三个“三”4.智慧的课堂要做好四个“主”5.智慧的课堂把握五个“原则”6.智慧的课堂坚持的六个“基本观点”10.智慧的课堂的十大“要素”8.智慧的课堂操作的八大“妙处”9.智慧的课堂推进的九个“程序”7.智慧的课堂操作的七个“技法”例1：如果一个角的两边分别平行于另一个角的两边，那么这两个角（）问题一：何时相等？何时互补？（一）专业技能：深入知识的本质，渗透数学思想，升华数学思维。问题二：你还能将它与我们学过的那些熟悉的知识联系在一起？问题三：你能发现这与代数有理数乘法符号法则的联系吗？AECDFBO1234如图所示，当CD//OB,EF//OA时，AOB4,3,2,1和相等或互补。结论：当两组平行边的射线方向全相同或全相反时，这两个角相等；两组平行边的射线方向一同一反时，这两个角互补。18042,31AOBAOBAOB即问题一：何时相等？何时互补？再进一步，如果将直线EF平移，使它与OA所在直线重合，如图2所示，由前所示，当然继续有.1,1802,3AOBAOBAOB但这时，上述关系，不分别是“两直线平行，则同位角相等；两直线平行，则同旁内角互补；两直线平行，则内错角相等吗？”BOECDF1234A知识间的联系，竟如此令人意想不到，却又是如此合情合理。问题二：你还能将它与我们学过的那些熟悉的知识联系在一起？不是平角的定义吗！互补及分别和定义”吗！相等，不也是“角相等和,423AOBAOB在图3的基础，把CD平移，使之与OB所在直线重合。那么，是对顶角相等！相等，竟然可同时认为和而1AOBOECDF1234BA这样分散在几何中有关角的40多条定义、定理中的6条定义、定理（角相等与平角定义、对顶角相等、两直线平行同位角相等、内错角相等、同旁内角互补）都包括在一条定理里，它们原本就是一和系统，置知识于系统中，着眼知识之间的联系.问题二：你还能将它与我们学过的那些熟悉的知识联系在一起？AECDFBO1234如图所示，当CD//OB,EF//OA时，AOB4,3,2,1和相等或互补。进一步，如果再把两条射线方向相同的关系规定为“+”，方向相反的关系规定为“-”；把两个角相等的关系规定为“+”，互补的关系规定为“-”。那么，初一代数中有理数乘法的符号法则：同号得正，异号得负。不正描述了本定理的结论！问题三：你能发现这与代数有理数乘法符号法则的联系吗？优越性1：将知识置于一个系统中，着眼于知识之间的联系。在这个融会贯通的过程中，透过纷杂的现象，抓住了数学本质，简化记忆。（一）专业技能：深入知识的本质，渗透数学思想，升华数学思维。优越性2：交给学生认识问题的思想方法：由寻找联系入手，运用规定、平移、变换等思想和“特殊到一般，又从一般到特殊”的方法，把离散现象构...