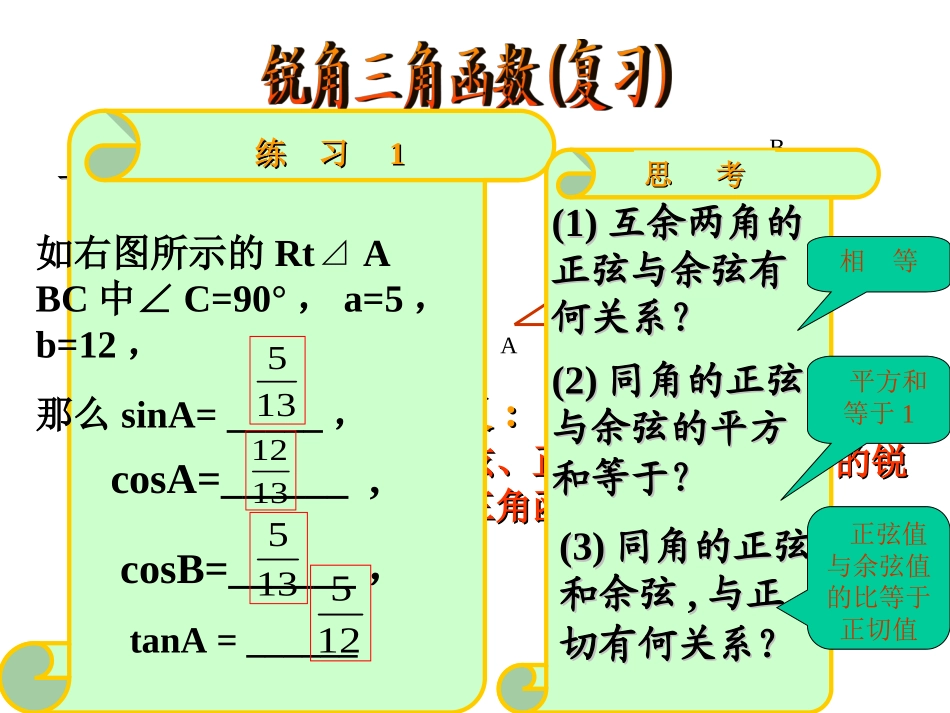
一、基本概念一、基本概念1.正弦ABCacsinA=ca2.余弦bcosA=cb3.正切tanA=ba锐角锐角AA的正弦、的正弦、余弦、正切、都叫做∠余弦、正切、都叫做∠AA的锐的锐角三角函数角三角函数..定义定义::练习练习11如右图所示的RtA⊿BC中∠C=90°,a=5,b=12,那么sinA=_____,tanA=______cosB=______,135125135cosA=______,思考思考1312(3)(3)同角的正弦同角的正弦和余弦和余弦,,与正与正切有何关系?切有何关系?正弦值与余弦值的比等于正切值(1)(1)互余两角的互余两角的正弦与余弦有正弦与余弦有何关系?何关系?(2)(2)同角的正弦同角的正弦与余弦的平方与余弦的平方和等于?和等于?平方和等于1相等sinA=cos(90°-A)=cosBcosA=sin(90°-A)=sinBcABCba同角的正弦余弦与正切和余切之间的关系互余两个角的三角函数关系同角的正弦余弦平方和等于1互为余角的两个角的正切互为倒数练习练习22二、几个重要关系式二、几个重要关系式tanA·tanB=1sin2A+cos2A=1⑴已知:RtABC△中,∠C=90°A∠为锐角,且tanA=0.6,tanB=().5/3⑵sin2A+tanAtanB-2+cos2A=()0⑶tan44°tan46°=().1(4)tan29°tan60°tan61°=().3(5)sin53°cos37°+cos53°sin37°=()1tanA=AAcossintanαcosαsinα60°45°30°角度三角函数三、特殊角三角函数值三、特殊角三角函数值21231角度逐渐增大正弦值如何变化?正弦值也增大余弦值如何变化?余弦值逐渐减小正切值如何变化?正切值也随之增大思思考考锐角A的正弦值、余弦值有无变化范围?045°时,sinA的值()(A)0<sinA<(B)<sinA<1(C)0<sinA<(D)<sinA<13.3.确定值的范确定值的范围围23222223B(A)0<cosA<(B)<cosA<1(C)0<cosA<(D)<cosA<1212123232.当锐角A>30°时,cosA的值()C☆☆应用练习应用练习1.1.已知角,求值已知角,求值确定角的范围确定角的范围2.2.已知值,求角已知值,求角3.3.确定值的范围确定值的范围(A)0°<∠A<30°(B)30°<∠A<90°(C)0°<∠A<60°(D)60°<∠A<901.当∠A为锐角,且tanA的值大于时,∠A()33B4.4.确定角的范围确定角的范围32.当∠A为锐角,且tanA的值小于时,∠A()(A)0°<∠A<30°(B)30°<∠A<90°(C)0°<∠A<60°(D)60°<∠A<90°c☆☆应用练应用练习习1.1.已知角,求已知角,求值值2.2.已知值,求角已知值,求角3.3.确定值的范围确定值的范围3.当∠A为锐角,且cosA=那么()514.4.确定角的范确定角的范围围(A)0°<∠A<30°(B)30°<∠A≤45°(C)45°<∠A≤60°(D)60°<∠A<90°确定角的确定角的范围范围4.当∠A为锐角,且sinA=那么()31(A)0°<∠A<30°(B)30°<∠A<45°(C)45°<∠A≤60°(D)60°<∠A≤90°DA课后练习课后练习1.在△ABC中∠C=90°B=2A∠∠则cosA=______3.已A是锐角且tanA=3,则2.若tan(β+20°)=β为锐角则β=________3__sin2cos2cossinAAAA4.在RtABC△中,∠C=90°cosB=,则sinB的值为_______32412340°35思考思考在RtABC△中,∠C=90°斜边AB=2,直角边AC=1,∠ABC=30°,延长CB到D,连接AD使∠D=15°求tan15°的值。DACB1如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.ABC4503004cm2如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.ABC4503004cmD┌锐角三角函数的应用3如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.4如图,根据图中已知数据,求AD.ABC55025020D┌ABC55025020随堂练习5如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.6如图,根据图中已知数据,求AD.ABCβαaD┌ABCαβa随堂练习解直角三角形综合练习一张