正方形课件 (2)VIP免费

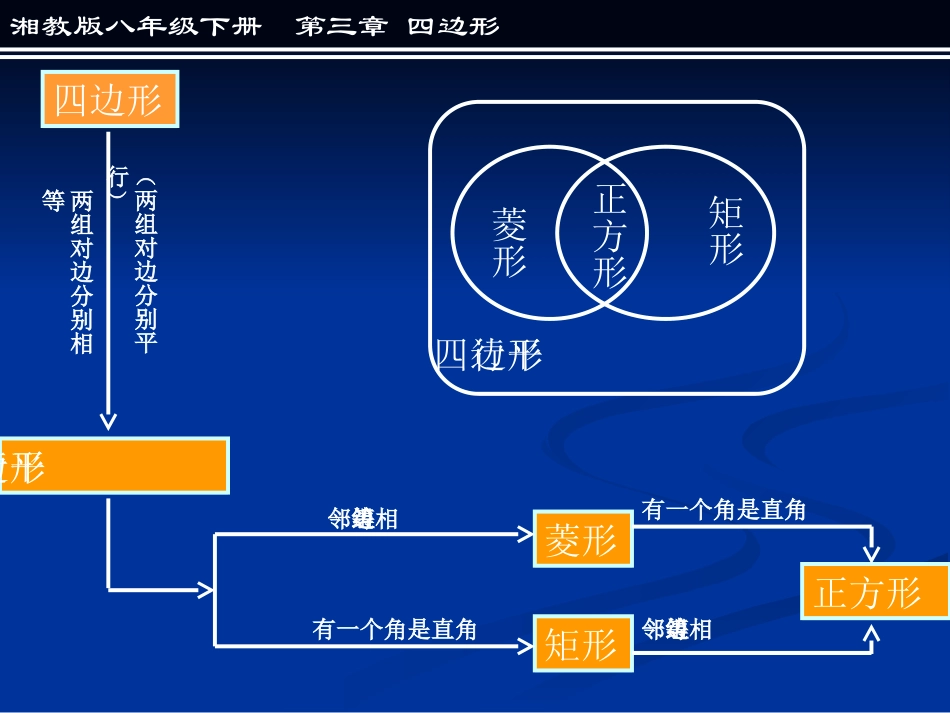
正方形正方形枫香九校：肖智忠枫香九校：肖智忠2009年4月湘教版八年级下册湘教版八年级下册XIANGJIAOBANBANIANJIXIACEXIANGJIAOBANBANIANJIXIACE菱形矩形四边形（两组对边分别平行）两组对边分别相等一组邻边相等有一个角是直角正方形有一个角是直角一组邻边相等平行四边形平行四边形菱形矩形正方形湘教版八年级下册第三章四边形ABCD一、正方形的定义：二、正方形的记法：2、用平行四边形定义：一组邻边相等，并且有一个角是直角的平行四边形叫做正方形。3、用菱形定义：有一个角是直角的菱形叫作正方形。4、用矩形定义：有一组邻边相等的矩形叫作正方形。1、用四边形定义：四条边相等，并且有一个角是直角的四边形叫作正方形。正方形用它的各个顶点的字母来表示。如图所示，可以按照顶点的顺序，记作正方形ABCD。湘教版八年级下册第三章四边形ABCDO1、从边来说，正方形的对边平行。四条边相等（即对边相等，邻边也相等）。2、从角来说，正方形的四个角都相等，并且都等于90。3、从对角线来说，4、从对称性来说，正方形不仅是中心对称图形，也是轴对称图形。三、正方形的性质：ENFM即：AB∥CD，AD∥BC。AB=BC=CD=AD即：∠DAB=∠ABC=∠BCD=∠CDA=90。即：AC与BD互相平分，即AO=CO，BO=DO。AC⊥BD，即：∠BOC=∠COD=∠AOD=90。AC平分∠DAB和∠BCD，BD平分∠ABC和∠CDA。正方形的对角线互相平分，互相垂直，两条对角线相等。并且每一条对角线平分一组对角。四、正方形的判定：湘教版八年级下册第三章四边形1、四条边相等，并且有一个角是直角的四边形是正方形。2、一组邻边相等，并且有一个角是直角的平行四边形是正方形。3、对角线相等且互相垂直平分的四边是是正方形。（也可以说，对角线相等且互相垂直的平行四边是是正方形。）4、有一个角是直角的菱形是正方形。5、有一组邻边相等的矩形是正方形。ABCDO动脑筋动脑筋动脑筋动脑筋湘教版八年级上册第三章四边形正方形ABCD被它的两条对角线AC、BD分成了四个三角形，它们是什么样的三角形，这些三角形全等吗？证明：由于ABCD是正方形，因此四边相等，对角线垂直平分且相等。故：AB=BC=CD=AD，A0=BO=CO=DO根据“边边边定理”从而△OAB、△OBC、△OCD、△ODA都是全等的等腰直角三角形。正方形的两条对角线AC、BD把正方形分成了四个等腰直角三角形，并且这四个三角形是全等的。结论：正方形的四边对角线把正方形分成了八个全等的等腰直角三角形。EFMN（2）画一个正方形，使它的对角线长为2cm,并且求它的边长。试一试试一试试一试试一试湘教版八年级下册第三章四边形（1）画一个正方形，使它的边长为2cm，并且求它的对角线的长。根据勾股定理，该正方形的对角线长：22CDBCBD根据勾股定理，该正方形的对角线长为2cm,因此AO=BO=1cm。所以边长：22BOAOAB2cm2cmABCD222282222112ABCDO以前我们学过求正方形的面积的方法，知道正方形的面积等于边长的平方。议一议议一议议一议议一议湘教版八年级下册第三章四边形2ABSABCD正方形222ADCDBCABCD如果在一个正方形中，我们知道对角线的长，可以直接用对角线乘积的一半来计算正方形的面积。OBDACSABCD2正方形22BD22AC例题例题例题例题（1）DE=DF吗？为什么？（2）只添加一个条件，使四边形EDFA是正方形。（不另外添加辅助线，无需说明理由）湘教版八年级下册第三章四边形（1）解：连结AD。相等，因为AB=AC，因此三角形ABC是等腰三角形，故AD是等腰三角形的中线。根据三线合一，AD也是顶角∠BAC的角平分线。又由于DE⊥AB，DF⊥AC，所以，DE=DF（角平分线上的点到角两边的距离相等）（方法不唯一）如图，在△ABC中，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为E、F。（2）解：可以添加∠A=90。（或∠EDF=90。）还可以添加AE∥DF（或AF∥DE），还可以添加AF=DF（或AE=DE）ABCDFE1.已知正方形的一条边长为1cm,求它的对角线长。2.已知正方形的一条对角线长为4cm，求它的边长、周长和面积。3.如图所示，∠CAB是多少度？为什么？至少用两种方法说明理由。1.练习练习练习练习湘教版八年级下册第三章四边形22.边长=cm，C=cm，S=8cm2283.45度。22课堂小结课堂小结课...