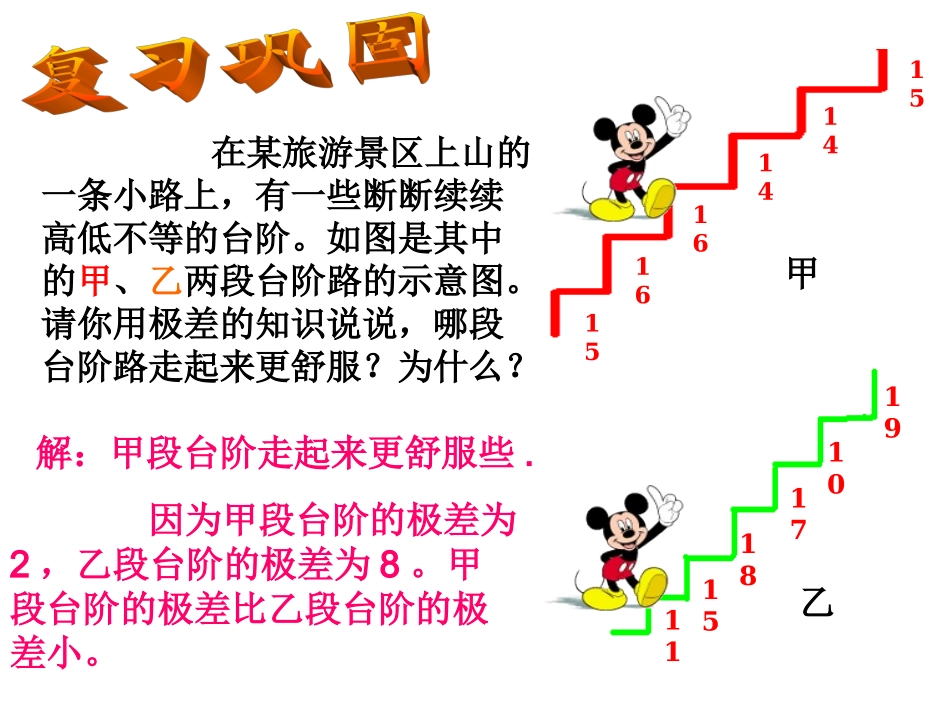
在某旅游景区上山的一条小路上,有一些断断续续高低不等的台阶。如图是其中的甲、乙两段台阶路的示意图。请你用极差的知识说说,哪段台阶路走起来更舒服?为什么?151616141415111518171019甲乙解:甲段台阶走起来更舒服些.因为甲段台阶的极差为2,乙段台阶的极差为8。甲段台阶的极差比乙段台阶的极差小。怎样才能衡量整个一组数据的波动大小呢?导入新课20.2.2方差第一次第二次第三次第四次第五次甲命中环数78889乙命中环数1061068甲,乙两名射击手的测试成绩统计如下:⑴请分别计算两名射手的平均成绩;教练的烦恼ÒÒx=8(环)=8(环)甲x甲,乙两名射击手现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较适宜?教练的烦恼第一次第二次第三次第四次第五次甲命中环数78889乙命中环数1061068012234546810甲,乙两名射击手的测试成绩统计如下:成绩(环)射击次序(1)请根据这两名射击手的成绩在下图中画出折线统计图;教练的烦恼(2)现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较适宜?为什么?第一次第二次第三次第四次第五次甲命中环数78889乙命中环数1061068012234546810甲,乙两名射击手的测试成绩统计如下:成绩(环)射击次序⑴请分别计算两名射手的平均成绩;⑵请根据这两名射击手的成绩在下图中画出折线统计图;⑶现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较适宜?为什么?教练的烦恼甲射击成绩与平均成绩的偏差的和:乙射击成绩与平均成绩的偏差的和:(7-8)+(8-8)+(8-8)+(8-8)+(9-8)=0(10-8)+(6-8)+(10-8)+(6-8)+(8-8)=0(10-8)2+(6-8)2+(10-8)2+(6-8)2+(8-8)2=(7-8)2+(8-8)2+(8-8)2+(8-8)2+(9-8)2=甲射击成绩与平均成绩的偏差的平方和:乙射击成绩与平均成绩的偏差的平方和:找到啦!有区别了!216上述各偏差的平方和的大小还与什么有关?——与射击次数有关!进一步用各偏差平方的平均数来衡量数据的稳定性在样本容量相同的情况下方差越小,波动越小,越稳定.方差越大,波动越大,越不稳定.方差意义(或作用):用来衡量一批数据的波动大小.(即这批数据偏离平均数的大小).S2=[(x1-x)2+(x2-x)2+…+(xn-x)2]1n方差定义:各数据与它们的平均数的差的平方的平均数.计算方差的步骤可概括为“先平均,后求差,平方后,再平均”.方差的性方差的性质质::(1)(1)数据的方差都是非负数数据的方差都是非负数,,即即(2)(2)当且仅当每个数据都相等时当且仅当每个数据都相等时,,方差方差为零为零,,反过来反过来,,若若;02s.0212xxxsn,则注意几点(1)研究离散程度可用2S(2)方差应用更广泛衡量一组数据的波动大小(3)方差主要应用在平均数相等或接近时(4)方差大波动大,方差小波动小,一般选波动小的1、样本方差的作用是()(A)表示总体的平均水平(B)表示样本的平均水平(C)准确表示总体的波动大小(D)表示样本的波动大小3、在样本方差的计算公式数字10表示,数字20表示.)20(2...)20(22)20(121012sxnxx2、样本5、6、7、8、9的方差是.D2样本平均数样本容量练习一甲团乙团在一次芭蕾舞比赛中在一次芭蕾舞比赛中,,甲、乙两个芭蕾舞团表演甲、乙两个芭蕾舞团表演了舞剧《天鹅湖》了舞剧《天鹅湖》,,参加表演的女演员的身高参加表演的女演员的身高((单位单位:cm):cm)分别是分别是甲团甲团163164164165165165166167163164164165165165166167乙团乙团163164164165166167167168163164164165166167167168哪个芭蕾舞团女演员的身高更整齐哪个芭蕾舞团女演员的身高更整齐??165816716631652164163x甲166816821671661652164163x乙38.18)165167()165164()165163(s2222甲38)166168()166164()166163(s2乙解:甲乙两团女演员的身高分别是:22乙甲ss所以,甲芭蕾舞团女演员的身高更整齐。1.计算下列各组数据的方差:(1)6666666;(2)5566677;(3)3346899;(4)3336999;练习二2.一个样本的方差是零,若中位数是a,则它的平均数是()(A)等于a(B)不等于a(C)大于a(...