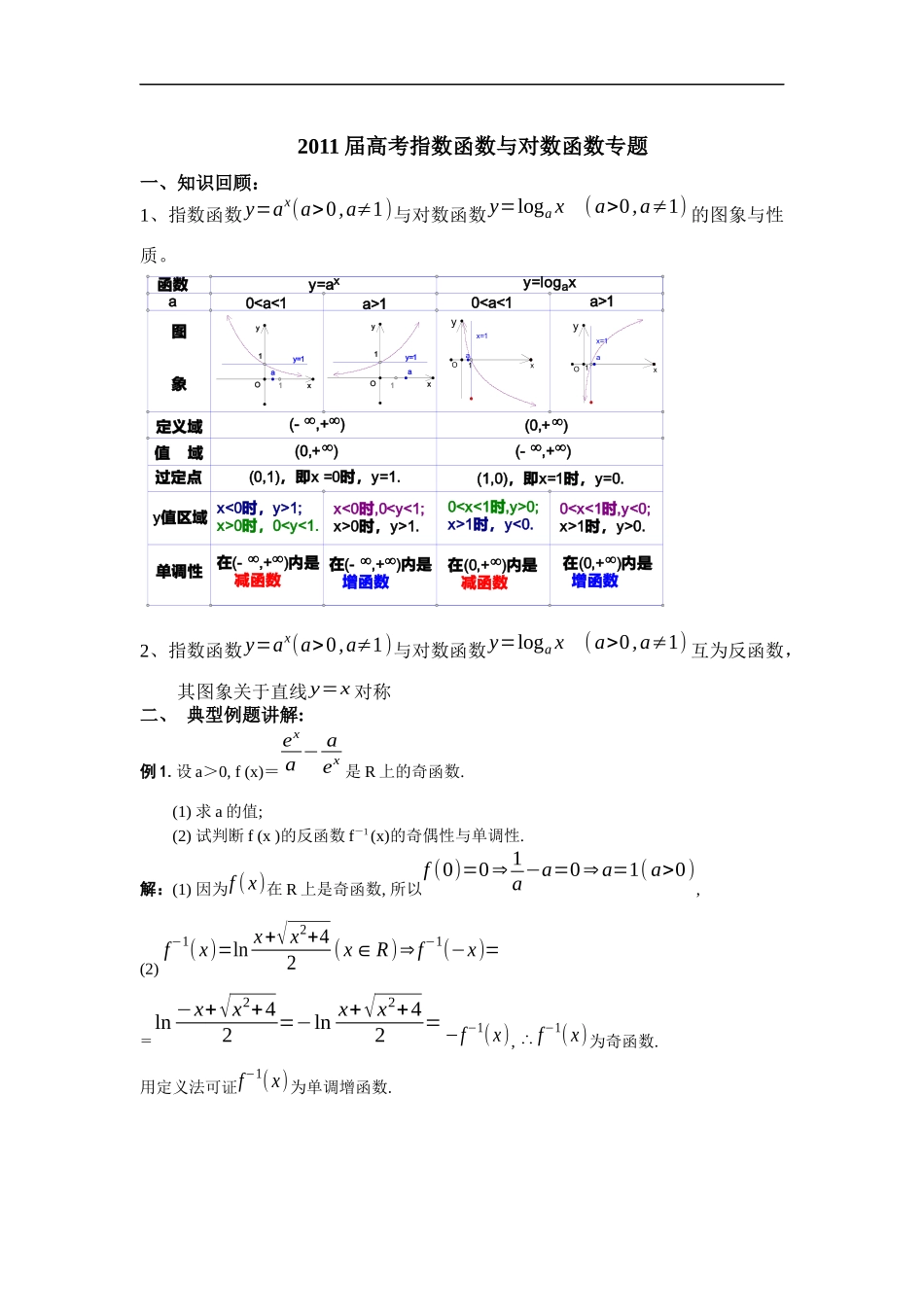
2011届高考指数函数与对数函数专题一、知识回顾:1、指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)的图象与性质。x=1x=1y=1y=1在(0,+)内是减函数在(0,+)内是增函数在(-,+)内是减函数在(-,+)内是增函数0
1时,y>0.00;x>1时,y<0.x<0时,00时,y>1.x<0时,y>1;x>0时,010100,a≠1)与对数函数y=logax(a>0,a≠1)互为反函数,其图象关于直线y=x对称二、典型例题讲解:例1.设a>0,f(x)=exa−aex是R上的奇函数.(1)求a的值;(2)试判断f(x)的反函数f-1(x)的奇偶性与单调性.解:(1)因为f(x)在R上是奇函数,所以f(0)=0⇒1a−a=0⇒a=1(a>0),(2)f−1(x)=lnx+√x2+42(x∈R)⇒f−1(−x)==ln−x+√x2+42=−lnx+√x2+42=−f−1(x),∴f−1(x)为奇函数.用定义法可证f−1(x)为单调增函数.例2.是否存在实数a,使函数f(x)=loga(ax2−x)在区间[2,4]上是增函数?如果存在,说明a可以取哪些值;如果不存在,请说明理由.解:设u(x)=ax2−x,对称轴x=12a.(1)当时,{12a≤2¿¿¿¿;(2)当a>1时,{12a≥4¿¿¿¿.综上所述:a>1三、历年高考题:1.(安徽卷文7)设232555322555abc(),(),(),则a,b,c的大小关系是(A)a>c>b(B)a>b>c(C)c>a>b(D)b>c>a【答案】A【解析】25yx在0x时是增函数,所以ac,2()5xy在0x时是减函数,所以cb。2.(湖南卷文8)函数y=ax2+bx与y=||logbax(ab≠0,|a|≠|b|)在同一直角坐标系中的图像可能是【答案】D【解析】对于A、B两图,|ba|>1而ax2+bx=0的两根之和为-ba,由图知0<-ba<1得-11矛盾,选D。3.(辽宁卷文10)设525bm,且112ab,则m(A)10(B)10(C)20(D)100【答案】D解析:选A.211log2log5log102,10,mmmmab又0,10.mm4.(全国Ⅰ卷理8文10)设a=3log2,b=In2,c=125,则A.af(1)=1+21=3,即a+2b的取值范围是(3,+∞).6.(全国Ⅰ卷文7)已知函数()|lg|fxx.若ab且,()()fafb,则ab的取值范围是(A)(1,)(B)[1,)(C)(2,)(D)[2,)【答案】C【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a的取值范围,而利用均值不等式求得a+b=12aa,从而错选D,这也是命题者的用苦良心之处.7.(山东卷文3)函数2log31xfx的值域为A.0,B.0,C.1,D.1,【答案】A【解析】因为311x,所以22log31log10xfx,故选A。【命题意图】本题考查对数函数的单调性、函数值域的求法等基础知识。8.(陕西卷文7)下列四类函数中,个有性质“对任意的x>0,y>0,函数f(x)满足f(x+y)=f(x)f(y)”的是[](A)幂函数(B)对数函数(C)指数函数(D)余弦函数【答案】C【解析】因为xyxyaaa所以f(x+y)=f(x)f(y)。9.(上海卷文17)若0x是方程式lg2xx的解,则0x属于区间[答]()(A)(0,1).(B)(1,1.25).(C)(1.25,1.75)(D)(1.75,2)解析:04147lg)47()75.1(,2lg)(ffxxxf由构造函数10....