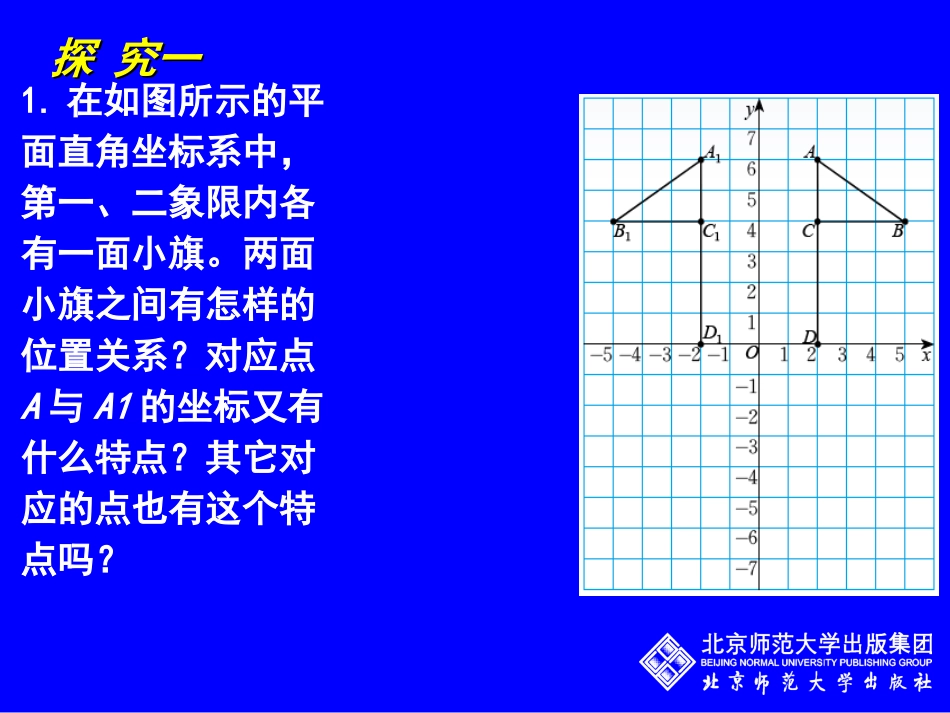
第三章位置与坐标3.轴对称与坐标变化1.在如图所示的平面直角坐标系中,第一、二象限内各有一面小旗。两面小旗之间有怎样的位置关系?对应点A与A1的坐标又有什么特点?其它对应的点也有这个特点吗?探究一探究一2.在这个坐标系里画出小旗ABCD关于X轴的对称图形,它的各个“顶点”的坐标与原来的点的坐标有什么关系?ABCC2B2A2D2D归纳概括在平面直角坐标系中:1.关于x轴对称的两点,它们的横坐标相同,纵坐标互为相反数;2.关于y轴对称的两点,它们的横坐标互为相反数,纵坐标相同。例题:已知点P(a-1,3),A(2,b+1),(1)如果点P与点A关于x轴对称,那么a=b=_______(2)如果点P与点A关于y轴对称,那么a=b=_____。3-4-12探究二:1.在直角坐标系中描出以下各点:(0,0)(5,4)(3,0)(5,1)(5,-1)(3,0)(4,-2)(0,0),并用线段依次连接,你得到了一个怎样的图案?123456780–1–2–3–4–512349105yx2.将所得图案的各个“顶点”的纵坐标保持不变,横坐标分别乘-1,依次连接这些点你会得到怎样的图案?这个图案与原图案又有怎样的位置关系呢?12345-1-2-30–1–2–3–4–51234-4-55yx顶点坐标的变化:(x,y)(0,0)(5,4)(3,0)(5,1)(5,-1)(3,0)(4,-2)(0,0)(-x,y)(0,0)(-5,4)(-3,0)(-5,1)(-5,-1)(-3,0)(-2,-2)(0,0)猜一猜将原图案的各个“顶点”的横坐标保持不变,纵坐标分别乘-1,依次连接这些点,你会得到怎样的图案?这个图案与原图案有怎样的位置关系?123456780–1–2–3–4–512345yx(x,y)(0,0)(5,4)(3,0)(5,1)(5,-1)(3,0)(4,-2)(0,0)(x,-y)(0,0)(5,-4)(3,0)(5,-1)(5,1)(3,0)(4,2)(0,0)归纳概括横坐标互为相反数相同纵坐标相同互为相反数结论关于y轴对称关于x轴对称巩固练习1.点A(2,-3)关于x轴对称的点的坐标是().2.点B(-2,1)关于y轴对称的点的坐标是().3.点(4,3)与点(4,-3)的关系是().A.关于原点对称B.关于x轴对称C.关于y轴对称D.不能构成对称关系4.点(m,-1)和点(2,n)关于y轴对称,则mn等于()A.-2B.2C.1D.-12,32,1BB5.王明是班上公认的“小马虎”,在做作业时,将点A的横纵坐标次序颠倒,写成A(a,b),小华也不细心,将点B的坐标写成关于y轴的对称点的坐标,写成B(-b,-a),则A,B两点原来的位置关系是()A,关于y轴对称B,关于x轴对称C,A和B重合D,以上都不对6.将△ABC的纵坐标不变,横坐标都乘以-1,则所得图形与原图形的关系是()。7.点P(-2,3)关于y轴的对称点是Q,则PQ的长是()B关于y轴对称41、关于y轴对称的两个图形上点的坐标特征:(x,y)(-x,y)2、关于x轴对称的两个图形上点的坐标特征:(x,y)(x,-y)小结归纳–5图中的鱼是将坐标为:(0,0)(5,4)(3,0)(5,1)(5,-1)(3,0)(4,-2)(0,0)的点用线段依次连接而成的。将各坐标的纵坐标与横坐标都乘以-1,图形会变成什么样?yx234510–1–2–3–412345–1–2–3–4–5坐标变化为:(x,y)(0,0)(5,4)(3,0)(5,1)(5,-1)(3,0)(4,-2)(0,0)(-x,-y)(0,0)(-5,-4)(-3,0)(-5,-1)(-5,1)(-3,0)(-4,2)(0,0)归纳在平面直角坐标系内,关于原点对称的两个点的坐标:横纵坐标都互为相反数。巩固练习1.设点M(1,2)关于原点的对称点为N,则N的坐标为()2.点A的坐标为(-5,3),点A与点B关于x轴对称,点C与点B关于原点对称,则C点的坐标为()。-1,-25,3作业布置•教材3.5习题1,2,3,4题