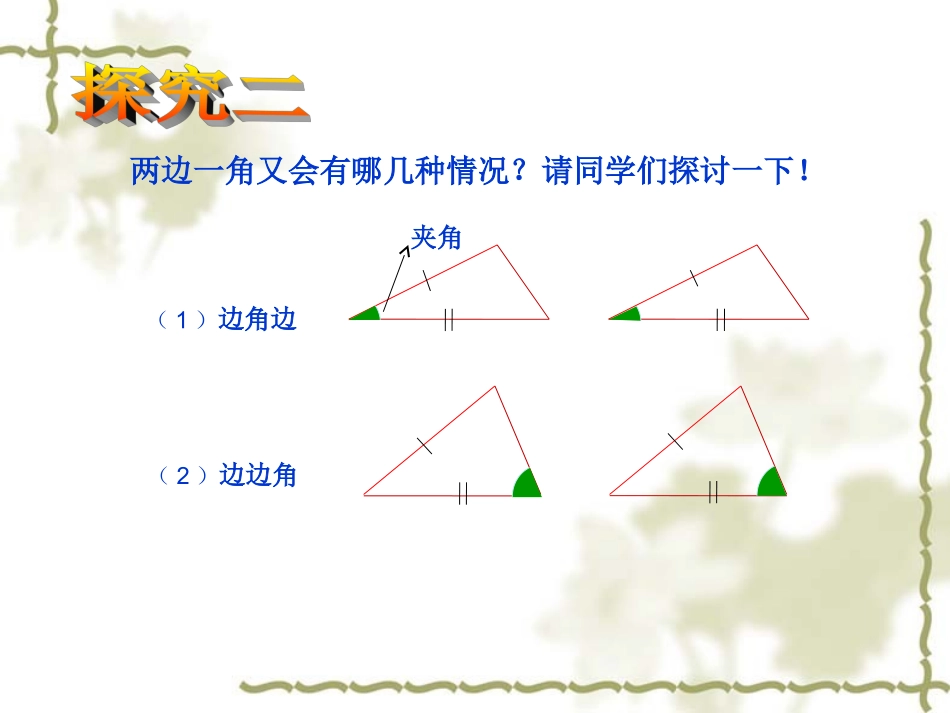
19.2全等三角形的判定(一)边角边(SAS)探讨:如果两个三角形有三组对应相等的元素,那么会有几种可能的情况?两边一角两边一角两角一边两角一边三角三角三边三边两边一角又会有哪几种情况?请同学们探讨一下!(2)边边角(1)边角边夹角“边角边”是否能够判断两个三角形全等呢?下面我们来探讨一下!边角边夹角如图,已知两条线段和一个角,已这两条线段为边,以这个角为这两条边的夹角,画一个三角形。9cm12cm画法:1.画∠MAN=45°2.在射线AM上截取AB=12cm3.在射线AN上截取AC=9cm4.连接BC∴△ABC就是所求的三角形把你所画的三角形剪下来与其他同学所画的三角形进行比较,我们能发现什么?B12cmC9cm45°NAM45°如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等.简记S.A.S.(或边角边)结论:三角形全等判定方法三角形全等判定方法用符号语言表达为:在△ABC与△A`B`C`中AB=A`B`∠B=B`∠BC=B`C`∴△ABCA`B`C`≌△(S.A.S.)A′ABCB′C′例题:如图,在△ABC中,AB=AC,AD平分∠BAC,求证:ABDACD△≌△∠BAD=CAD,∠证明:∵AD平分∠BAC∴∠BAD=CAD∠在△ABD与△ACD中,AB=AC,AD=AD,∴△ABDACD≌△(S.A.S.)ABCD试一试:已知:如图,AB=AC,AD=AE.求证:△ABE≌△ACDACDBEA证明:在△ABE和△ACD中AB=AC(已知)∠A=∠A(公共角)AD=AE(已知)∴△ABE≌△ACD(S.A.S.)“边边角”是否能够判断两个三角形全等呢?下面我们来探讨一下!边边角以9cm,12cm为三角形的两边,长度为9cm的边所对的角为45°,情况又怎样?动手画一画,你发现了什么?ABCDEF9cm12cm45°45°12cm结论:两边及其一边所对的角相等,两个三角形不一定全等9cm9cm1、根据题目条件,判断下面的三角形是否全等.(1)AC=DF,∠C=∠F,BC=EF(2)BC=BD,∠ABC=∠ABDAABBCCFFDDAABBCCDD((全等全等))((全等全等))(1)(2)1、根据题目条件,判断下面的三角形是否全等.(1)AC=DF,∠C=∠F,BC=EF(2)BC=BD,∠ABC=∠ABDAABBCCDD(1)(2)E2、点M是等腰梯形ABCD底边AB的中点,求证:△AMDBMC≌△ABCDM证明:在等腰梯形ABCD中有AD=BC,∠A=B∠又∵点M是AB的中点∴AM=BM在△AMD和△BMC中AD=BC∠A=B∠AM=BM∴△AMDBMC≌△(S.A.S.)(S.A.S.)已知:如图,AD∥BC,AD=CB.求证:△ADC≌△CBAABCD12证明:∵AD∥BC∴∠1=∠2(两直线平行,内错角相等)在△ADC和△CBA中AD=CB(已知)∵∠1=∠2(已证)AC=CA(公共边)∴△ADC≌△CBA(S.A.S.)2.用SAS判定三角形全等的注意点:(1)至少需要三个条件(2)必须是两边一夹角(如不是夹角,则不一定全等)(3)全等的三个条件必须是三角形的对应边和对应角,如条件不完整,则必须先证明三个条件。1.三角形全等的条件,两边和它们的夹角对应相等的两个三角形全等(边角边或SAS)作业:课本79页第2题第4题