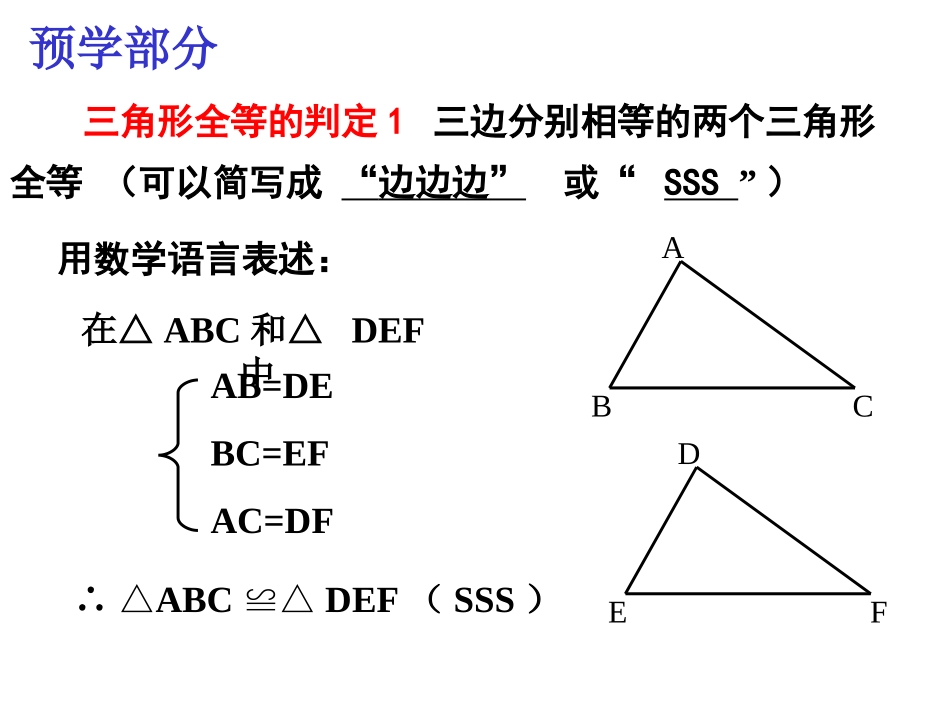
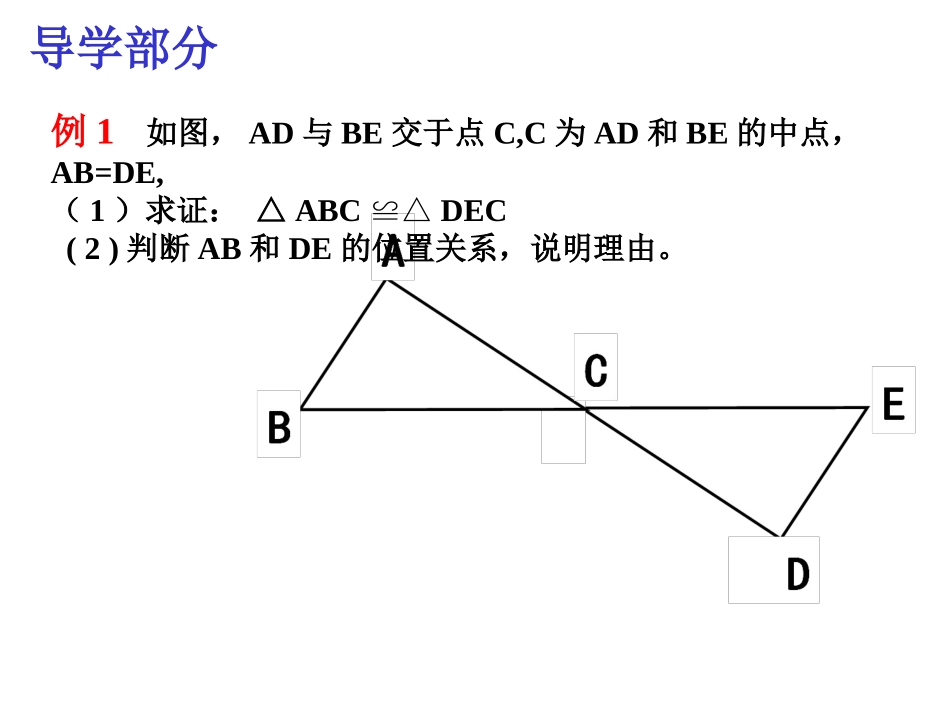
12.2三角形全等的判定(一)三角形全等的判定1三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”)ABCDEF用数学语言表述:在△ABC和△DEF中∴△ABCDEF≌△(SSS)AB=DEBC=EFAC=DF预学部分导学部分例1如图,AD与BE交于点C,C为AD和BE的中点,AB=DE,(1)求证:△ABCDEC≌△(2)判断AB和DE的位置关系,说明理由。导学部分变题如图,点B、F、C、E在一直线上,AB=DE,AC=DF,BF=CE.(1)求证:△ABCDEF≌△(2)判断AB和DE的位置关系,说明理由。ABC导学部分变题如图,点B、F、C、E在一直线上,AB=DE,AC=DF,BF=CE.(1)求证:△ABCDEF≌△(2)判断AB和DE的位置关系,说明理由。变题如图,如图,AB=DC,AD=BC.求证:∠A=∠C.BCAD练习1如图,△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架。AD与BC垂直吗?为什么?DCBA练习2如图,点B、D、C、E在一条直线上,△ABDACE,≌△图中还有其它的全等三角形吗?如果有,请写出来并证明你的结论。BCADE练习3如图,AB=DC,AC=DB,求证:∠A=∠DCABDO如果△ABC的三边长分别为5、6、8,△DEF的三边长分别为5、x+y、x-y,试问当x和y为何值时,△ABC与△DEF全等?悟学部分3.转化与分类讨论的思想方法.课堂小结2.“SSS”这一判定方法的应用;1.三边分别相等的两个三角形全等(SSS);作法:(1)以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D;已知:∠AOB.求作:∠A′O′B′=∠AOB.用尺规作一个角等于已知角.ODBCA拓展应用作法:(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;已知:∠AOB.求作:∠A′O′B′=∠AOB.用尺规作一个角等于已知角.O′C′A′ODBCA作法:(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;已知:∠AOB.求作:∠A′O′B′=∠AOB.用尺规作一个角等于已知角.O′D′C′A′ODBCA作法:(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.已知:∠AOB.求作:∠A′O′B′=∠AOB.用尺规作一个角等于已知角.O′D′B′C′A′ODBCA作法:(1)以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D;(2)画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;(3)以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;(4)过点D′画射线O′B′,则∠A′O′B′=∠AOB.已知:∠AOB.求作:∠A′O′B′=∠AOB.用尺规作一个角等于已知角.