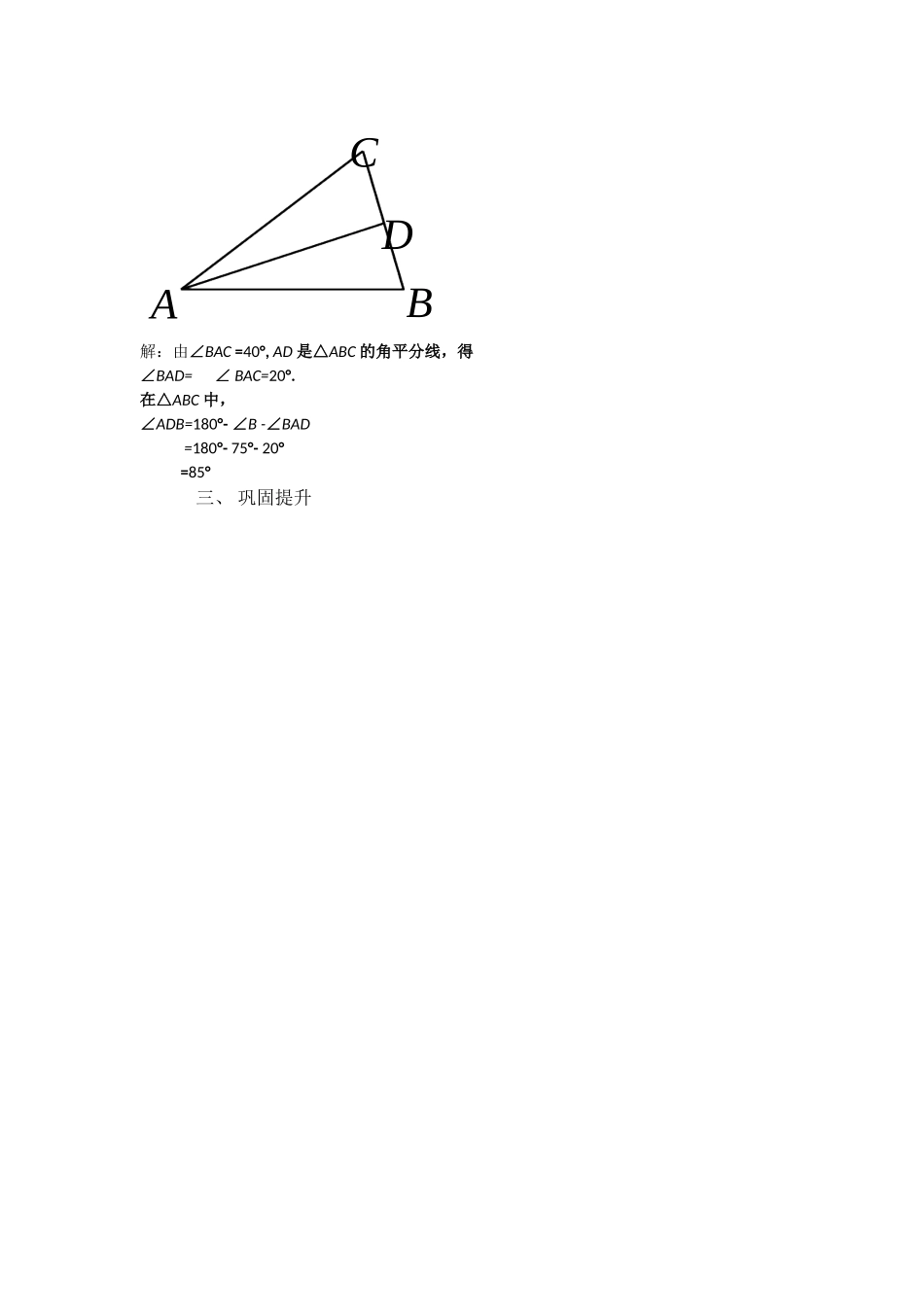
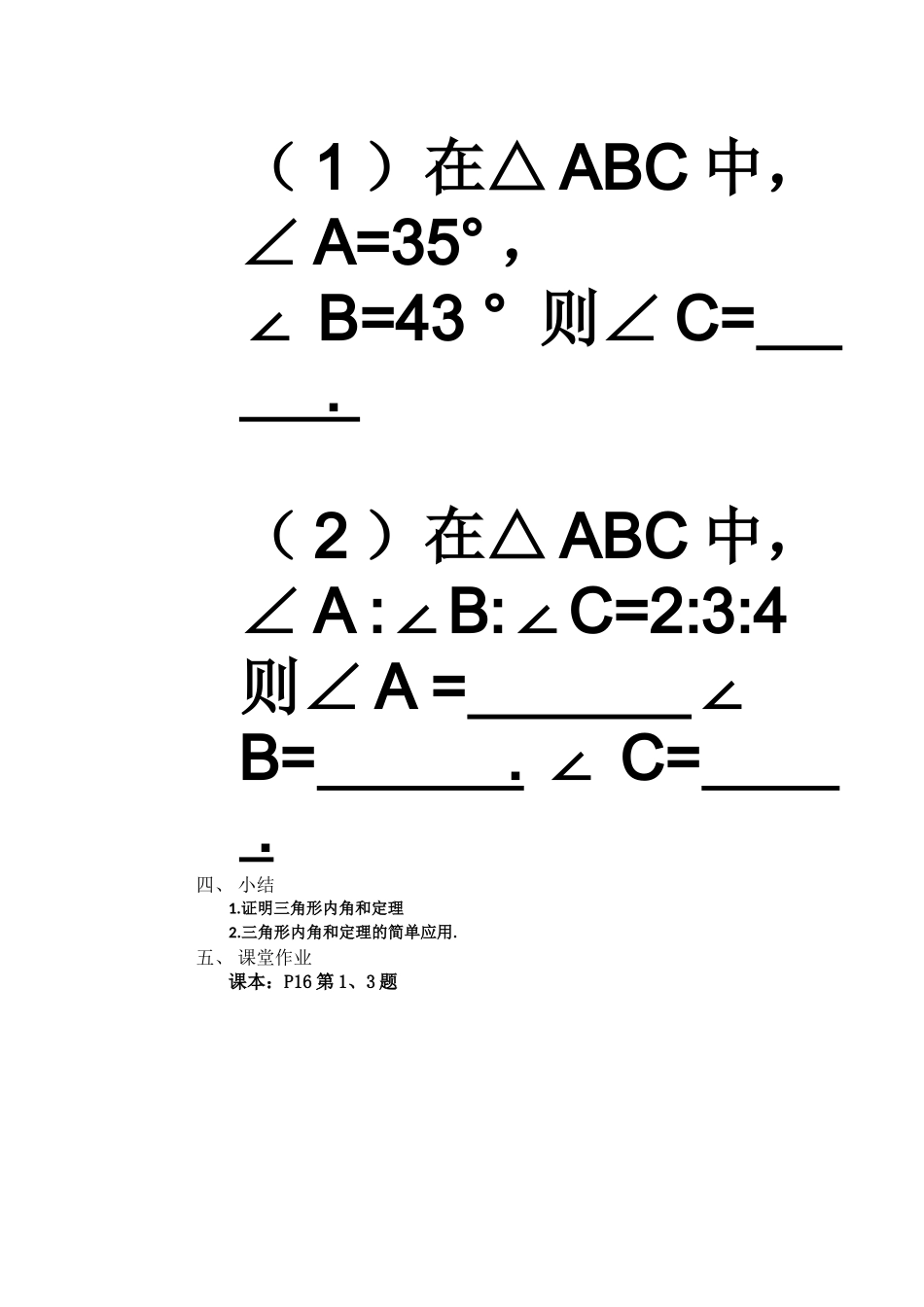
教学设计教学目标:1经历实验活动的过程,得出三角形的内角和定理,能用平行线的性质推出这一定理。2能应用三角形内角和定理及性质解决一些简单的实际问题。3通过证明三个的角和为180°,转化为一个平角,让学生了解这种转化的数学思想在数学中的应用。教学重点、难点:重点:三角形内角和定理、性质及应用难点:三角形内角和定理的推理的过程课前准备:每人准备一个三角形一、创设情景,提出问题三角形的内角和是多少度?(180度)怎么利用手中的三角形,来验证一下,你的结论。将三角形的三个角撕下来,通过拼接转化到一个平角,自己动手实验,尝试不同的拼凑方法。二、新知讲授利用刚刚拼接的过程,怎样去证明,三角形内角和是180度。已知:△ABC,可以利用平行线转化为平角,也可以利用同旁内角互补例1如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线.求∠ADB的度数.求证:∠A+∠B+∠C=180°CBA解:由∠BAC=40°,AD是△ABC的角平分线,得∠BAD=∠BAC=20°.在△ABC中,∠ADB=180°-∠B-∠BAD=180°-75°-20°=85°三、巩固提升CBDA四、小结1.证明三角形内角和定理2.三角形内角和定理的简单应用.五、课堂作业课本:P16第1、3题(1)在△ABC中,∠A=35°,∠B=43°则∠C=.(2)在△ABC中,∠A:B:C=2:3:4∠∠则∠A=∠B=.C=∠.