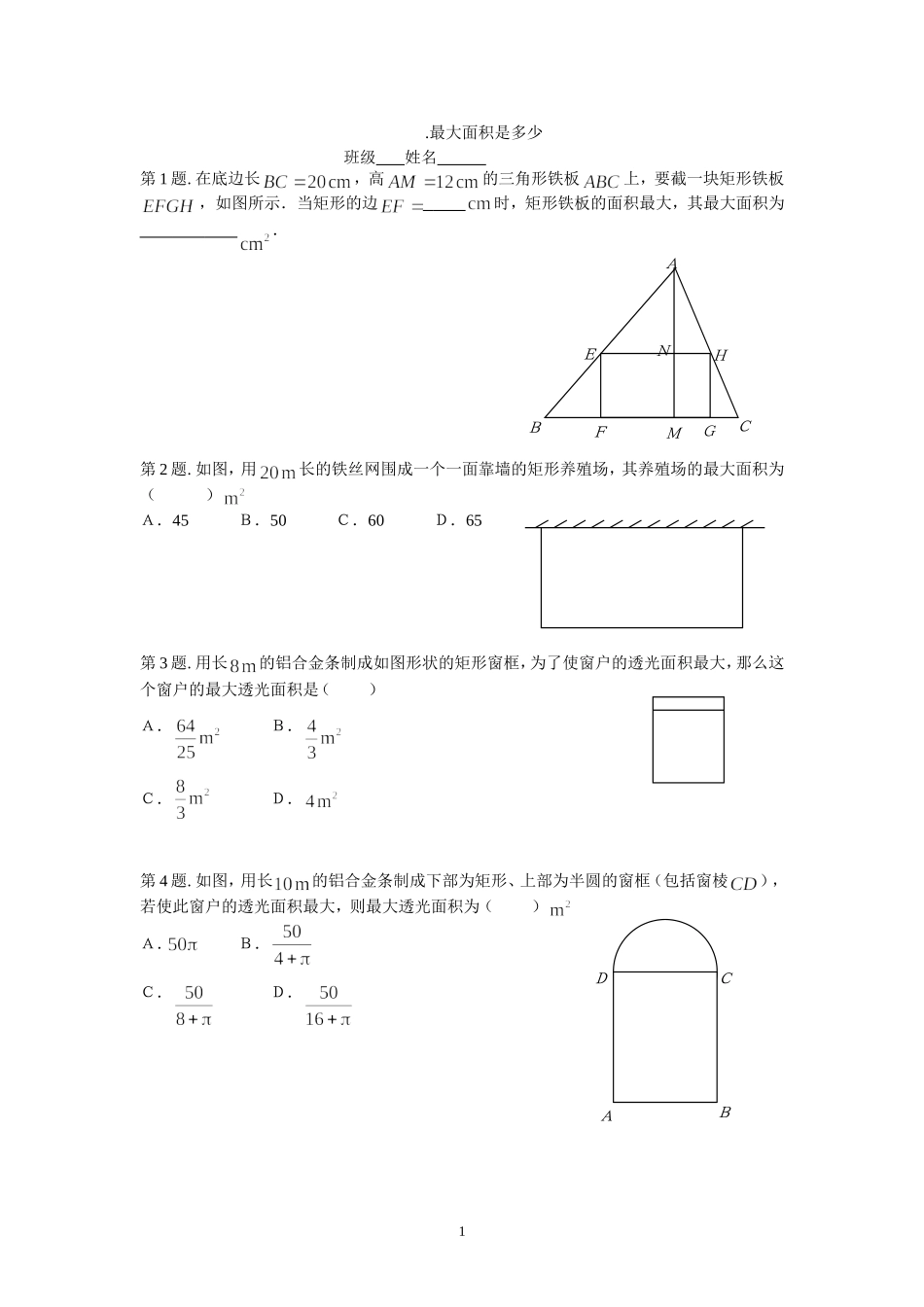
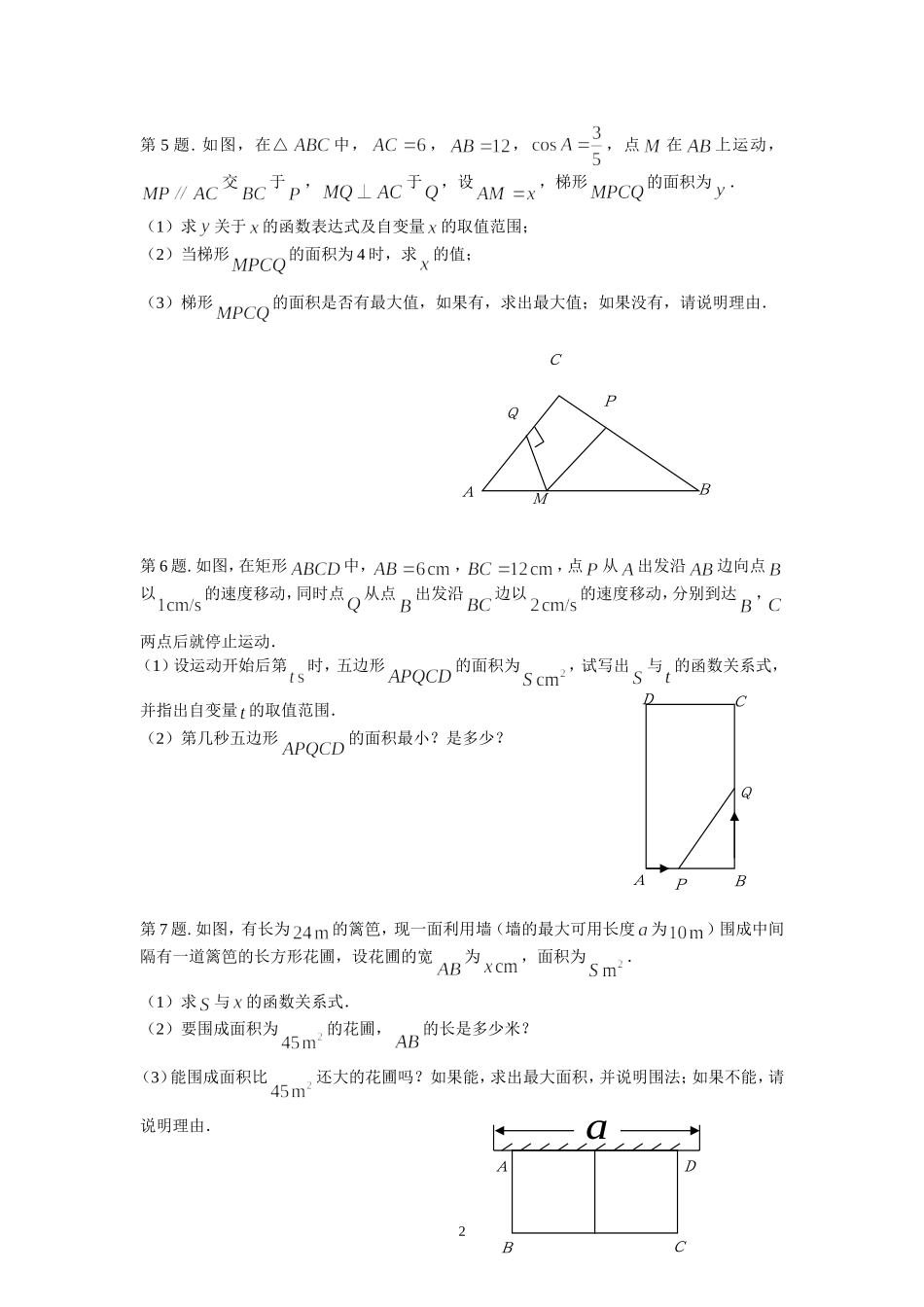
.最大面积是多少班级姓名第1题.在底边长,高的三角形铁板上,要截一块矩形铁板,如图所示.当矩形的边时,矩形铁板的面积最大,其最大面积为.第2题.如图,用长的铁丝网围成一个一面靠墙的矩形养殖场,其养殖场的最大面积为()A.45B.50C.60D.65第3题.用长的铝合金条制成如图形状的矩形窗框,为了使窗户的透光面积最大,那么这个窗户的最大透光面积是()A.B.C.D.第4题.如图,用长的铝合金条制成下部为矩形、上部为半圆的窗框(包括窗棱),若使此窗户的透光面积最大,则最大透光面积为()A.B.C.D.1AEBFMGCHNDCBA第5题.如图,在△中,,,,点在上运动,交于,于,设,梯形的面积为.(1)求关于的函数表达式及自变量的取值范围;(2)当梯形的面积为4时,求的值;(3)梯形的面积是否有最大值,如果有,求出最大值;如果没有,请说明理由.第6题.如图,在矩形中,,,点从出发沿边向点以的速度移动,同时点从点出发沿边以的速度移动,分别到达,两点后就停止运动.(1)设运动开始后第时,五边形的面积为,试写出与的函数关系式,并指出自变量的取值范围.(2)第几秒五边形的面积最小?是多少?第7题.如图,有长为的篱笆,现一面利用墙(墙的最大可用长度为)围成中间隔有一道篱笆的长方形花圃,设花圃的宽为,面积为.(1)求与的函数关系式.(2)要围成面积为的花圃,的长是多少米?(3)能围成面积比还大的花圃吗?如果能,求出最大面积,并说明围法;如果不能,请说明理由.2CPBMAQDCQBPAaBADC第8题.如图,在Rt△中,,,,点在斜边上,分别作于,于,设,.(1)求与之间的函数关系,并求出的取值范围.(2)设四边形的面积为,试求的最大值.第9题.某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现,年销售量(万件)与销售单位(元)之间存在着如图所示的一次函数关系.(1)求关于的函数关系式;(2)试写出该公司销售该种产品的年获利(万元)关于销售单价(元)的函数关系式(年获利=年销售额-年销售产品总进价-年总开支).当销售单价为何值时,年获利最大?并求这个最大值;(3)若公司希望该种产品一年的销售获利不低于40万元,借助(2)中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?3AECFBD020406080123456(万件)(元)第10题、今年我省干旱灾情严重,甲地急需要抗旱用水15万吨,乙地13万吨.现有A、B两水库各调出14万吨水支援甲、乙两地抗旱.从A地到甲地50千米,到乙地30千米;从B地到甲地60千米,到乙地45千米.⑴设从A水库调往甲地的水量为x万吨,完成下表甲乙总计Ax14B14总计151328⑵请设计一个调运方案,使水的调运量尽可能小.(调运量=调运水的重量×调运的距离,单位:万吨•千米)第10题、A市有某种型号的农用车50辆,B市有40辆,现要将这些农用车全部调往C、D两县,C县需要该种农用车42辆,D县需要48辆,从A市运往C、D两县农用车的费用分别为每辆300元和150元,从B市运往C、D两县农用车的费用分别为每辆200元和250元.(1)设从A市运往C县的农用车为x辆,此次调运总费为y元,求y与x的函数关系式,并写出自变量x的取值范围;(2)若此次调运的总费用不超过16000元,有哪几种调运方案?哪种方案的费用最小?并求出最小费用?第11题、某市百货商店服装部在销售中发现“米奇”童装平均每天可售出20件,每件获利40元。为了迎接“六一”儿童节和扩大销售,增加利润,商场决定采取适当的降价措施,经过市场调查,发现如果每件童装每降价1元,则平均每天可多售出2件,要想平均每天在销售这种童装上获利1200元,那么每件童装应降价多少元?要想获得最大利润,每件童装应该卖多少元?4调入地水量/万吨调出地