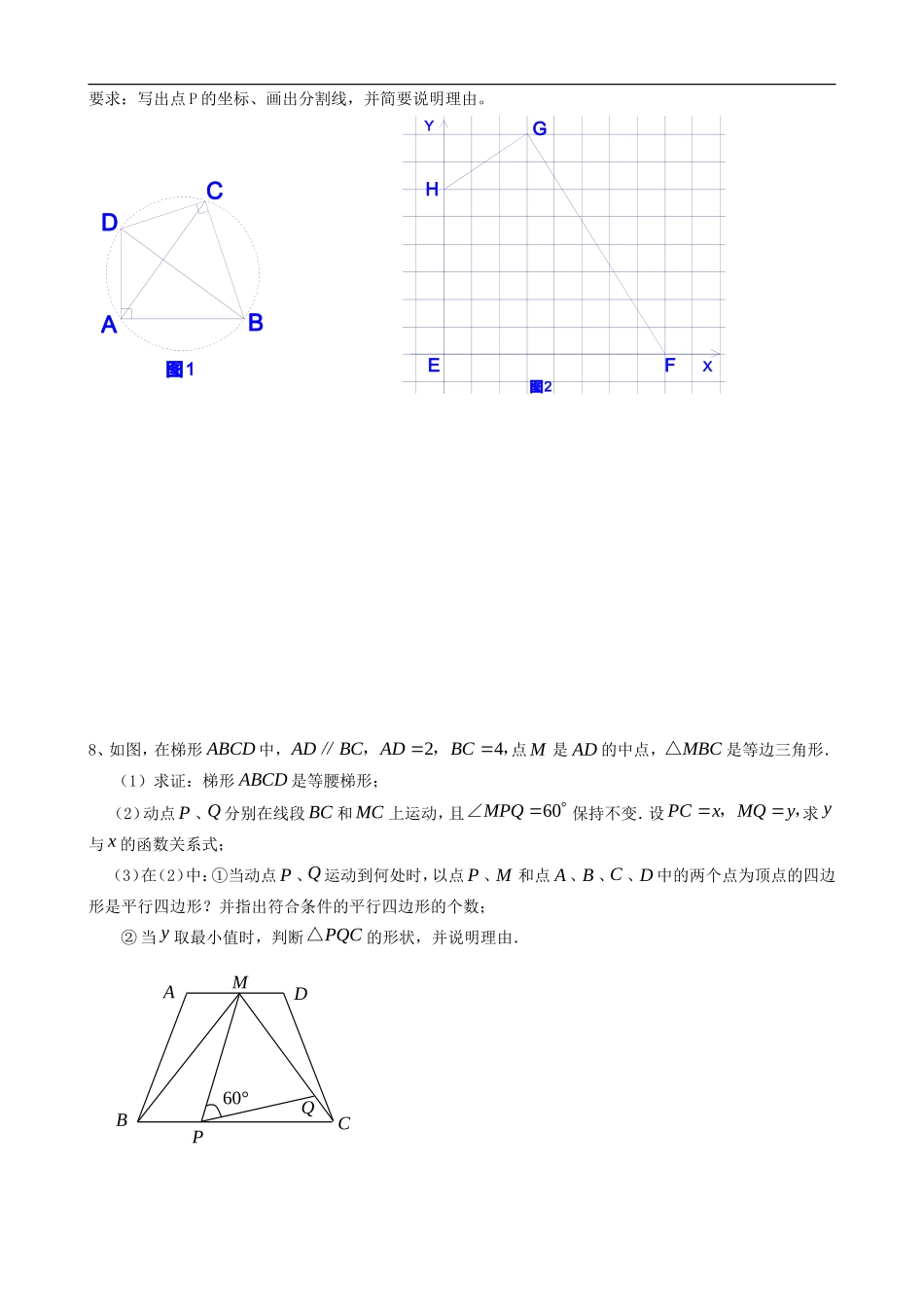
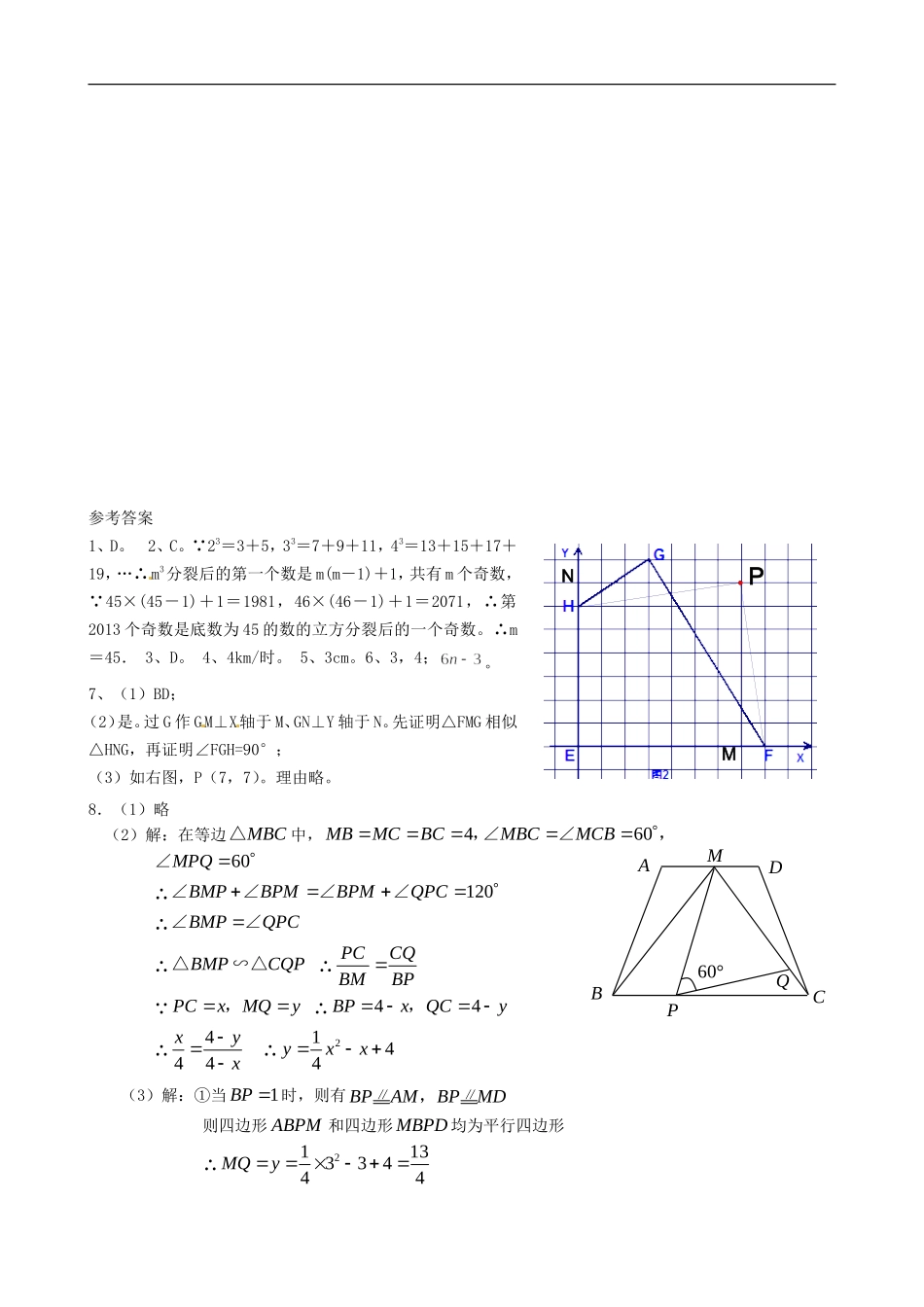
广东省顺德一中德胜学校2013届九年级数学尖子生资料4北师大版2、大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是2013,则m的值是()A.43B.44C.45D.463、小翔在如图1所示的场地上匀速跑步,他从点A出发,沿箭头所示的方向经过B跑到点C,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翊跑步的时间为t(单位:秒),他与教练距离为y(单位:米),表示y与t的函数关系的图象大致如图2,刚这个固定位置可能是图1的()A.点MB.点NC.点PD.Q图1图24、如上右图,射线OA、BA分别表示甲、乙两人骑自行车运动过程的一次函数的图象,图中s、t分别表示行驶距离和时间,则这两人骑自行车的速度相差。5、如图,△ABC中,∠ACB=90°,AB=8cm,D是AB的中点.现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,则GH的长等于。6、在平面直角坐标系中,我们把横纵坐标都是整数点的叫做整点.已知点A(0,4),点B是x正半轴上的整点,记△AOB内部(不包括边界)的整数点个数为m,当时,点B的横坐标的所有可能值是_______;当点B的横坐标为(n为正整数)时,____________.(用含n的代数式表示)7、图1是只有一组对角为直角的四边形(我们规定这一类四边形的集合为M),连结它的两个非直角顶点的线段叫做这个四边形的“直径”(相当于经过这个四边形的四个顶点的圆的直径)。(1)识图:如图1,四边形ABCD的直径是线段;(2)判断:如图2,在坐标系中(网络小方格的单位长为1)的四边形EFGH是否为M中的四边形?给出简要说明;(3)思考、操作并解决问题:在图2中找到一个点P,使四边形EFPH为M中的四边形,并且这个四边形用一条直线分割成两块后可以拼成一个正方形。QNMPCBAO30t/秒y/米1、要求:写出点P的坐标、画出分割线,并简要说明理由。图1DCBAYXHGFE图28、如图,在梯形ABCD中,24ADBCADBC∥,,,点M是AD的中点,MBC△是等边三角形.(1)求证:梯形ABCD是等腰梯形;(2)动点P、Q分别在线段BC和MC上运动,且60MPQ∠保持不变.设PCxMQy,,求y与x的函数关系式;(3)在(2)中:①当动点P、Q运动到何处时,以点P、M和点A、B、C、D中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;②当y取最小值时,判断PQC△的形状,并说明理由.ADCBPMQ60°参考答案1、D。2、C。∵23=3+5,33=7+9+11,43=13+15+17+19,…∴m3分裂后的第一个数是m(m-1)+1,共有m个奇数,∵45×(45-1)+1=1981,46×(46-1)+1=2071,∴第2013个奇数是底数为45的数的立方分裂后的一个奇数。∴m=45.3、D。4、4km/时。5、3cm。6、3,4;。7、(1)BD;(2)是。过G作GM⊥X轴于M、GN⊥Y轴于N。先证明△FMG相似△HNG,再证明∠FGH=90°;(3)如右图,P(7,7)。理由略。NMP8.(1)略(2)解:在等边MBC△中,4MBMCBC,60MBCMCB∠∠,60MPQ∠∴120BMPBPMBPMQPC∠∠∠∠∴BMPQPC∠∠∴BMPCQP△∽△∴PCCQBMBP∵PCxMQy,∴44BPxQCy,∴444xyx∴2144yxx(3)解:①当1BP时,则有BPAMBPMD∥∥,则四边形ABPM和四边形MBPD均为平行四边形∴211333444MQyADCBPMQ60°当3BP时,则有PCAMPCMD∥∥,则四边形MPCD和四边形APCM均为平行四边形∴11311444MQy∴当1314BPMQ,或1334BPMQ,时,以P、M和A、B、C、D中的两个点为顶点的四边形是平行四边形.此时平行四边形有4个.②PQC△为直角三角形∵21234yx∴当y取最小值时,2xPC∴P是BC的中点,MPBC,而60MPQ∠,∴30CPQ∠,∴90PQC∠