直线和圆锥曲线的参数方程VIP免费

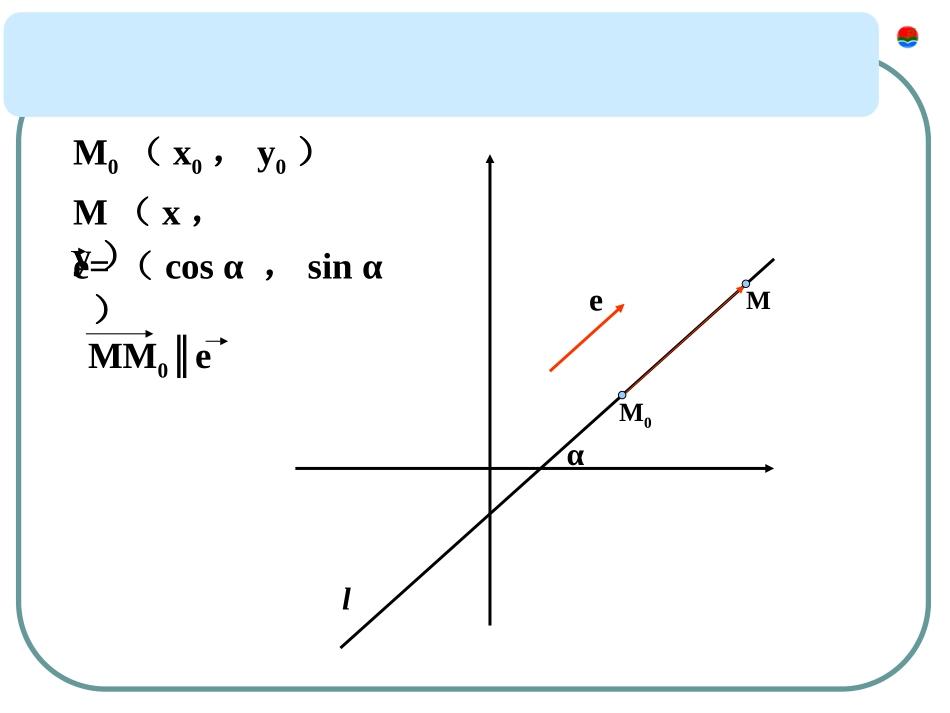
高二数学(下)新课引入学习目标新课讲解典型例题知识小结巩固练习作业eM0MlαM（x，y）MM0∥ee=（cosα，sinα）M0（x0，y0）直线的参数方程00cossinxxtyyt问：α的含义？问：参数t的含义？eM0Mlα直线的参数方程00cossinxxtyyt310xy例1：化直线l1的普通方程为参数方程，并说明参数的几何意义,说明∣t∣的几何意义.313txty例2：化直线l2的参数方程（t为参数）为普通方程，并求倾斜角，说明∣t∣的几何意义.3112332xtyt133txty例3：已知直线l过点M0（1，3），倾斜角为判断方程（t为参数）（t为参数）是否为直线的参数方程？如果是直线的参数方程，指出方程中的参数t是否具有标准形式中参数t的几何意义.和方程00xxatyybt0MM(1)当a2+b2=1时，则t的几何意义是有向线段的数量.2202222022()()axxabtabbyyabtab22abt（2）当a2+b2≠1时，则t不具有上述的几何意义.可化为令t=练习：1.直线3sin204cos20xtyt（t为参数）的倾斜角.342.写出经过点M0（－2，3），倾斜角为的直线的标准参数方程，并且求出直线上与点M0相距为2的点的坐标.3.已知直线l的参数方程是(1)画出直线,指出t=-1对应的点p;(2)求p到M(-1,2)的距离;(3)求l的倾斜角;132xtyt例4已知直线l:x+y-1=0与抛物线y=x2交于A,B两点，求线段AB的长和点M(-1,2)到A,B两点的距离之积.探究:对于直线与曲线相交问题,例1的思路可行吗?直线与曲线若交于M1,M2两点，对应的参数分别为t1,t2.(1)曲线的弦M1M2的长是多少?(2)线段M1M2的中点M对应的参数t的值是多少?(3)你还能提出和解决哪些问题?例5已知直线l的参数方程是(1)画出直线,指出t=-1对应的点p;(2)求p到M(-1,2)的距离;(3)求l的倾斜角;(4)求l被曲线x2-y2=-3+4所截得弦长及中点坐标.3132xtyt例6经过点M(2,1)作直线l,交椭圆于两点A,B.如果点M恰好为线段AB的中点,求直线l的方程.221164xy探究:例2的解法对一般圆锥曲线适用吗?有其他方法吗？把“中点”改为“三等分点”，直线l的方程怎样求？例7当前台风中心P在某海滨城市O向东300km处生成，并以40km/h的速度向西偏北45°方向移动。已知距台风中心250km以内的地方都属于台风侵袭的范围，那么经过多长时间后该城市开始受到台风侵袭？MPOxy海滨城市O受台风侵袭大概持续多长时间?思考:上例中,如果台风侵袭的半径也发生变化(比如:当前半径为250km,并以10km/h的速度不断增大),那么问题又该如何解决?MPOxy例8如图所示,AB,CD是中心为O的椭圆的两条相交弦,交点为P.两弦AB,CD与椭圆长轴的夹角分别为∠1,2,∠且∠1=2.∠求证:|PA|·|PB|=|PC|·|PD|12OCDABP12OCDABP探究:如果把椭圆改为双曲线,是否会有类似的结论?