9.10整式的乘法VIP免费

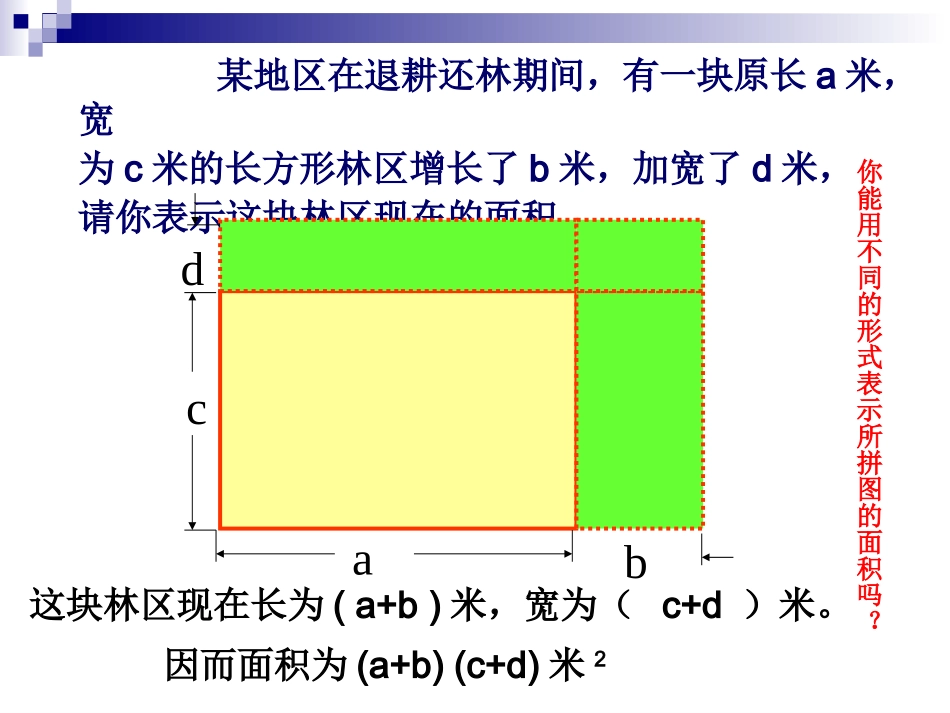
回顾与思考回顾回顾②②再把所得的积相加。再把所得的积相加。单项式与多项式相乘的单项式与多项式相乘的法则法则①①将将单项式分别乘以多项式的每一项，单项式分别乘以多项式的每一项，注意事项注意事项①①不能漏乘不能漏乘②②符号的确定符号的确定..计算：计算：-3a(-5+2a-a-3a(-5+2a-a22))某地区在退耕还林期间，有一块原长a米，宽为c米的长方形林区增长了b米，加宽了d米，请你表示这块林区现在的面积。cadb你能用不同的形式表示所拼图的面积吗？这块林区现在长为(a+b)米，宽为（c+d）米。因而面积为(a+b)(c+d)米2acadcadb这块林区现在长为（a+b）米，宽为（c+d）米,因而面积为(a+b)(c+d)米2这块林区现在的面积为(ac+ad+bc+bd)米2bcbdS1S2S4S3(a+b)(c+d)=ac+ad+bc+bd讨论探究(a+b)X=?(a+b)X=aX+bX(a+b)X=(a+b)(c+d)当X=c+d时,(a+b)X=?把(c+d)看成一个整体=ac+ad+bc+bd(a+b)(c+d)=a(c+d)+b(c+d)多项式多项式9.10(3)多项式与多项式相乘1234(a+b)(c+d)=ac1234+ad+bc+bd多项式与多项式相乘，先用一个多项式的每一项分别乘以另一个多项式的每一项，再把所得的积相加。多项式与多项式相乘的法则多项式与多项式相乘的法则例题解析【【例例11】】计算计算：：(1)(a+3)(b(1)(a+3)(b+5+5),(2)(3),(2)(3xx-y)(-y)(22xx+3y+3y))。。解解::(1)(1)(a+3)(b+5)(a+3)(b+5)（（2)(32)(3xx-y-y)(2)(2xx+3y)+3y)==6x6x22+9xy-2xy-3y+9xy-2xy-3y22=6x=6x22+7xy-3y+7xy-3y22=ab+5a+3b+15两项相乘时两项相乘时先定符号先定符号最后的结果最后的结果要合并同类要合并同类项项..随堂练习随堂练习(1)(1)(x+2)(x+3)(x+2)(x+3)(2)(2)(x+2)(x-3)(x+2)(x-3)(3)(3)(x-2)(x-3)(x-2)(x-3)计算：计算：第一轮第一轮（（11））(x(x22+1)(2-x+1)(2-x22))（（22））(x-2y)(x-2(x-2y)(x-2y)y)计算：计算：第二轮第二轮(1)((1)(xx--22yy))22切记:一般情况下(x-2y)2不等于x2-4y2.活动活动&&探探索索=(x-2y)(x-2y)=(x-2y)(x-2y)(2)(a-b)(a2+ab+b2)在合并同类项之前，展开式的项数恰好等于两个多项式的项数的积。(3)(x+y)(x–y)(x2+y2)三个多项式相乘，选其中的两个先相乘，把它们的积用括号括起来，再与第三个相乘。比一比：(1)(2a+3b)2(2)(a+b)(a2–ab+b2)(3)(m+1)(m–1)(m2+1)(4)(x+1)(x-2)(2x-1)注意：1、必须做到不重复，不遗漏.2、注意确定积中每一项的符号.3、结果应化为最简式(合并同类项合并同类项))方法与规方法与规律律方法与规方法与规律律填空：____)3)(2(2xxxx____)3)(2(2xxxx____)3)(2(2xxxx____)3)(2(2xxxx__________))((2xxbxax观察上面四个等式，你能发现什么规律？)(baab你能根据这个规律解决下面的问题吗？651(-6)(-1)(-6)(-5)6作业1）练习册P1911—142）思考题小东找来一张挂历画包数学课本．已知课本长a厘米，宽b厘米，厚c厘米，小东想将课本封面与封底的每一边都包进去m厘米，问小东应在挂历画上裁下一块多大面积的长方形？思考题：七年级第一学期数学cbaabcmbm面积：(2m+2b+c)(2m+a)解：(2m+2b+c)(2m+a)=4m2+2ma+4bm+2ab+2cm+ca答：小东应在挂历画上裁下一块（4m2+2ma+4bm+2ab+2cm+ca）平方厘米的长方形。挑战极限：如果(x2+bx+8)(x2–3x+c)的乘积中不含x2和x3的项，求b、c的值。解：原式=x4–3x3+cx2+bx3–3bx2+bcx+8x2–24x+8cX2项系数为：c–3b+8X3项系数为：b–3=0=0∴b=3,c=1