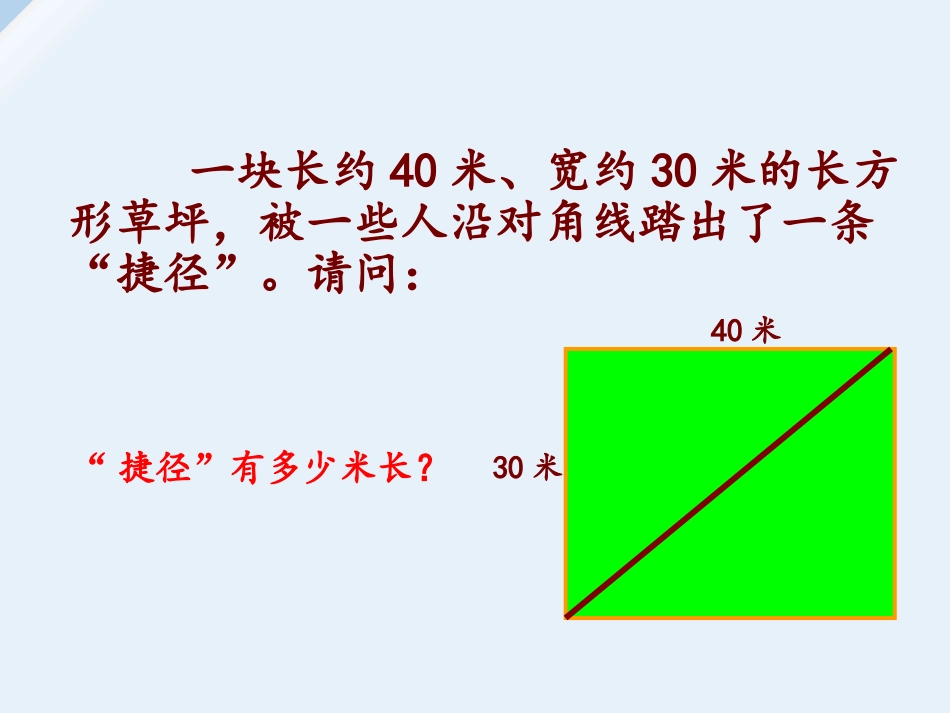
第8章认识概率陈春梅为什么要走“捷径”呢?一块长约40米、宽约30米的长方形草坪,被一些人沿对角线踏出了一条“捷径”。请问:“捷径”有多少米长?40米30米邮票赏析这是1955年希腊为纪念著名数学家毕达哥拉斯而发行的一张邮票实验1:将每个小正方形的面积看作1,△ABC是以格点为顶点的直角三角形,分别以三边向外作正方形。ABC以AB为边的正方形的面积是多少?SAC=9SBC=16实验基地实验基地ABCSAB253421449ABCSAB144312=25ABCSAC=9SBC=16SAB=25SAB=SAC+SBC实验2:在方格纸上,画一个顶点都在格点上的直角三角形;并分别以这个直角三角形的各边为一边向三角形外作正方形,然后仿照前面的方法计算以直角边、斜边为一边的正方形的面积.实验基地实验基地结论还成立吗?ABCA的面积+B的面积=C的面积abc如果直角三角形两直角边分别为a、b,斜边为c,那么a2+b2=c2直角三角形两直角边的平方和等于斜边的平方勾股定理西方称(毕达哥拉斯定理)abc确定斜边c2=a2+b2?acb确定斜边b2=a2+c2?bca确定斜边a2=b2+c2?温馨提醒温馨提醒1、在直角三角形中2、确定斜边数学文化数学文化我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。赵爽东汉末至三国时代吴国人,著有《勾股圆方圆说》。他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范。数学文化数学文化赵爽弦图第24届“国际数学家大会”(ICM)被誉为国际数学界的“奥林匹克”为2002北京“国际数学家大会”发行的纪念邮资明信片JP108例1:求下列直角三角形中未知边的长8x17125x解:在直角三角形中,由勾股定理可得:52+122=x2即:x2=52+122x=13解:在直角三角形中,由勾股定理可得:82+x2=172即:x2=172-82x=15例题精讲例题精讲用勾股定理建立方程.方法小结:例2:已知在直角三角形中,两直角边分别为3、4,则斜边是____________5例题精讲例题精讲变式1:已知在直角三角形中,两边分别为3、4,则第三条边的平方是____________25或7变式2:在Rt△ABC中,斜边AB=3,则AB2+BC2+AC2=____________2AB2=18例3:如图一块长为40米、宽为30米的长方形草坪,被一些人沿对角线踏出了一条“捷径”。请问:“捷径”比正路近多少米?例题精讲例题精讲在方格纸上,画一个顶点都在格点上的非直角三角形;并分别以这个三角形的各边为一边向三角形外作正方形,仿照前面的方法计算3个正方形的面积。能力提升能力提升回顾一下你本节课的学习,提出一个问题(可以是收获、发现、温馨提醒、困惑等)生活中不是缺少美,而是缺少发现美的眼睛。