模拟方法——概率的应用VIP免费

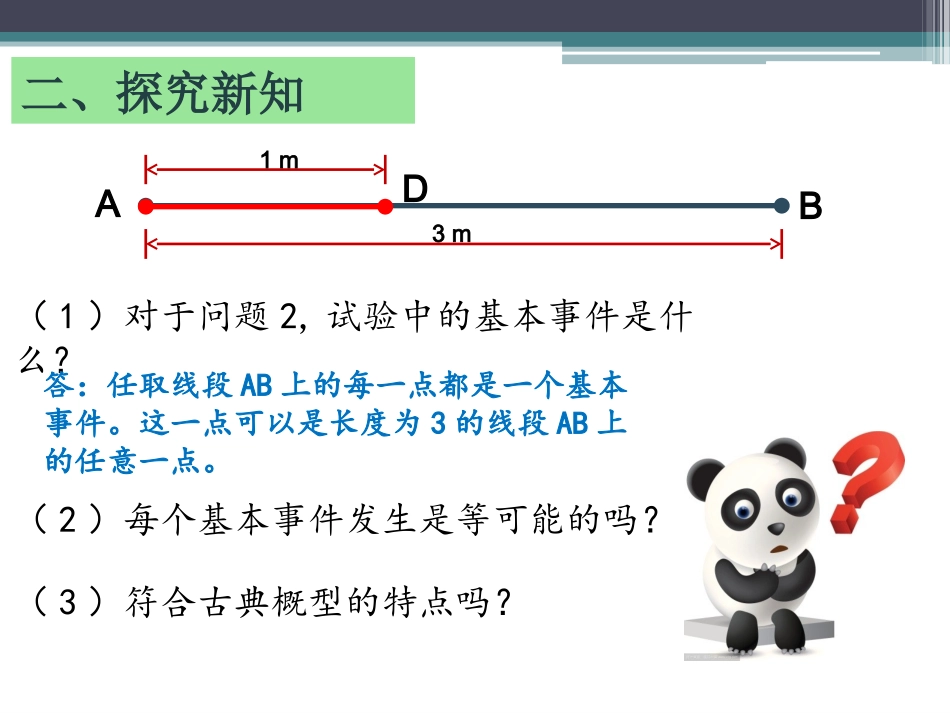
几何概型及其概率计算公式教师：孙恒宇学校：浮梁县第一中学一、思考与引入问题1：投掷一枚质地均匀的骰子，落地时向上点数为偶数的概率。回顾、思考：问：请回答，下列是不是古典概型问题？问题2：从长为3的线段AB上任取一点C，求满足的概率。1AC二、探究新知（1）对于问题2,试验中的基本事件是什么？答：任取线段AB上的每一点都是一个基本事件。这一点可以是长度为3的线段AB上的任意一点。（2）每个基本事件发生是等可能的吗？（3）符合古典概型的特点吗？AB3mD1m问题3：在边长为2的正方形内任取一点，这点到正方形中心的距离小于或等于1的概率。21二、探究新知（1）试验中的基本事件是什么？（2）每个基本事件发生是等可能的吗？（3）符合古典概型的特点吗？答：任取此正方形内的每一点都是一个基本事件。这一点可以是此边长为2的正方形内的任意一点。二、探究新知思考：二、探究新知上面两个试验有什么共同特点？1、试验中所有可能出现的结果（基本事件）有无限多个；2、每个基本事件出现的可能性相等。二、探究新知几何概型!二、探究新知几何概型的定义？二、探究新知几何概型：如果每个事件发生的概率只与构成该事件区域的长度（面积，或体积，或度数）成比例，则称这样的概率模型为几何概率模型。AB3mD1m21二、探究新知几何概型与古典概型的区别与联系：将古典概型中的总基本事件有限性推广到无限性，而保留等可能性，就得到几何概型。二、探究新知如何求解几何概型的概率？二、探究新知AB3mD1m问题2：从长为3的线段AB上任取一点C，求满足的概率。1AC解：记“满足”为事件A,则：1AC1==3APAADAB满足事件的点的活动区域长度此点可活动的全部区域长度的长度的长度问题3：在边长为2的正方形内任取一点，这点到正方形中心的距离小于或等于1的概率。21二、探究新知二、探究新知21解：记“这点到正方形中心的距离小于或等于1”为事件A,则：==4APASS圆正构成事件的点的区域面积此点的全部活动区域面积二、探究新知几何概型的概率公式？二、探究新知几何概型的概率计算公式：一般地，在几何区域D内随机取一点，记“该点落在其内部的一个区域d”为事件A，则：dPAD的测度的测度二、探究新知测度的意义：线段长度平面图形面积立体图形体积例题1：如图，正三棱锥S-ABC的底面边长为4，高为4。在此正三棱锥内任取一点P,则点P满足的概率为多少？12PABCSABCVVABCSO三、例题巩固ABCSO解：记“点P满足”为事件A，12PABCSABCVV如图，设三棱锥P-ABC的高为h,即PD=h,则：PD由得：12PABCSABCVV1114323ABCABCShS2h即：三、例题巩固ABCSOPDEFGH取SO的中点E，过点E作平行于底面ABC的截面FGH，则满足的点P的活动区域为棱台FGH-ABC内。12PABCSABCVV三、例题巩固ABCSOPDEFGH故有：FGHABCSABCVPAV三棱台三棱锥三、例题巩固1SABCSFGHSABCSFGHSABCVVVVV三棱锥三棱锥三棱锥三棱锥三棱锥11122343=1=111443378ABCFGHABCABCSSSS三、例题巩固求解几何概型问题的基本步骤？三、例题巩固几何概型的求解步骤：1、把基本事件空间转化为与之对应的区域D；2、把随机事件A转化为与之对应的区域d；3、利用几何概型概率公式计算：dPAD的测度的测度练一练：如图，三棱锥S-ABC的体积为V。在此三棱锥内任取一点P,则点P满足的概率为多少？13PABCSABCVVABCSO三、例题巩固答案：1927ABCSO解：记“点P满足”为事件A，13PABCSABCVV如图，设三棱锥P-ABC的高为h,即PD=h,则：PD由得：13PABCSABCVV111333ABCABCShSSO13hSO即：三、例题巩固ABCSOPDEFGH取SO的三等分点E，过点E作平行于底面ABC的截面FGH，则满足的点P的活动区域为棱台FGH-ABC内。13PABCSABCVV三、例题巩固ABCSOPDEFGH故有：1FGHABCSABCSABCSFGHSABCSFGHSABCVPAVVVVVV三棱台三棱锥三棱锥三棱锥三棱锥三棱锥三棱锥三、例题巩固13=113FGHABCSSESSO14421939=11193273ABCABCSSESSO...