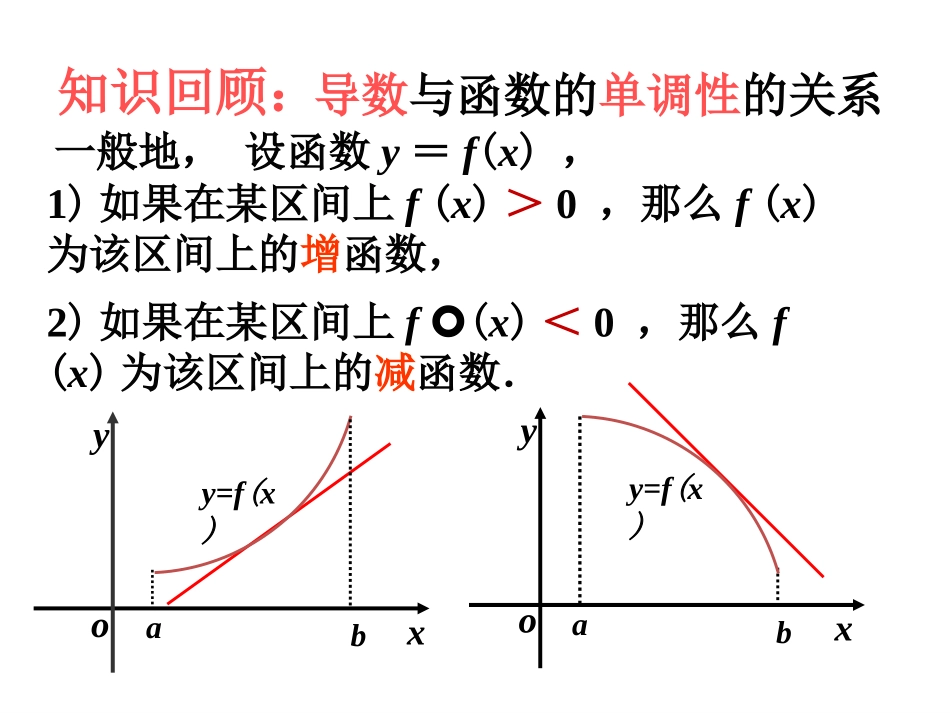
高中数学高中数学高中数学高中数学1)如果在某区间上f(x)>0,那么f(x)为该区间上的增函数,2)如果在某区间上f(x)<0,那么f(x)为该区间上的减函数.一般地,设函数y=f(x),aby=f(x)xoyy=f(x)xoyab导数与函数的单调性的关系知识回顾:(2)求导数f(x)(1)求y=f(x)的定义域D(4)与定义域求交集利用导数讨论函数单调的步骤:(5)写出单调区间(3)解不等式f(x)>0;或解不等式f(x)<0.基本求导公式:忆一忆(1)(kx+b)=k(k,b为常数),特殊地:C=0(C为常数)(2)(xα)=αxα-1(α为常数)(3)(ax)=axlna(a>0,且a≠1)(4)(logax)=logae=(a>0,且a≠1)1x1lnxa(5)(ex)=ex(6)(lnx)=1x(7)(sinx)=cosx(8)(cosx)=-sinx(问题情境)观察下图中P点附近图象从左到右的变化趋势、P点的函数值以及点P位置的特点.oax1x2x3x4bxyP(x1,f(x1))y=f(x)Q(x2,f(x2))函数图象在P点附近从左侧到右侧由“上升”变为“下降”(函数由单调递增变为单调递减),在P点附近,P点的位置最高,函数值最大函数极值的定义一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)﹤f(x0),我们就说f(x0)是函数f(x)的一个极大值,记作y极大值=f(x0);如果对x0附近的所有的点,都有f(x)﹥f(x0),我们就说f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0).极大值与极小值同称为极值.数学建构(1)极值是某一点附近的小区间而言的,是函数的局部性质,不是整体的最值;(2)函数的极值不一定惟一,在整个定义区间内可能有多个极大值和极小值;(3)极大值与极小值没有必然关系,极大值可能比极小值还小.学生活动oax1x2x3x4bxyP(x1,f(x1))y=f(x)Q(x2,f(x2))(1)极值是函数的最值吗?(2)函数的极值只有一个吗?(3)极大值一定比极小值还大吗?xx0左侧x0x0右侧f(x)f(x)观察图象并类比于函数的单调性与导数关系的研究方法,看极值与导数之间有什么关系?oax0bxy增f(x)=0f(x)<0极大值减f(x)>0数学建构oax0bxyxx0左侧x0x0右侧f(x)f(x)f(x)>0f(x)<0f(x)=0增减极小值请问如何判断f(x0)是极大值或是极小值?左正右负为极大,右正左负为极小函数y=f(x)的导数y/与函数值和极值之间的关系为()A导数y/由负变正,则函数y由减变为增,且有极大值B导数y/由负变正,则函数y由增变为减,且有极大值C导数y/由正变负,则函数y由增变为减,且有极小值D导数y/由正变负,则函数y由增变为减,且有极大值D学生活动例1:求f(x)=x2-x-2的极值.解:x)(xf)(xf21)21,(),21(0)21(f极小值因此,当x=时,f(x)有极小值f()=-.212194f(x)=2x-1,令f(x)=0,解得x=.列表:21的极值求函31431:23xxf(x)数例小试牛刀篇(数学运用)f(x)f(x)x∴当x=2时,y极小值=-5;当x=-2时,y极大=.(-∞,-2)-2(-2,2)2(2,+∞)+00-+极大值极小值-5173173解:∵f(x)=x2-4,由f(x)=0解得x1=2,x2=-2.当x变化时,f(x)、f(x)的变化情况如下表:小吃篇求下列函数的极值.xxy11)(16128223xxxy-)(探索:x=0是否为函数f(x)=x3的极值点?渐入佳境篇xyOf(x)=x3若寻找可导函数极值点,可否只由f(x)=0求得即可?f(x)=3x2,当f(x)=0时,x=0,而x=0不是该函数的极值点.f(x0)=0x0是可导函数f(x)的极值点.x0左右侧导数异号x0是函数f(x)的极值点f(x0)=0注意:f/(x0)=0是函数取得极值的必要不充分条件.请思考求可导函数的极值的步骤:④检查在方程=0的根的左右两侧的符号,确定极值点.(最好通过列表法)①确定函数的定义域;②求导数)(xf③求方程)(xf=0的根,这些根也称为可能极值点;)(xf)(xf一览众山小强调:要想知道x0是极大值点还是极小值点就必须判断f(x0)=0左右侧导数的符号.一吐为快篇(小结)本节课主要学习了哪些内容?请想一想?1.极值的判定方法.2.极值的求法.注意点:1.f/(x0)=0是函数取得极值的必要不充分条件2.数形结合以及函数与方程思想的应用3.要想知道x0是极大值点还是极小值点就必须判断f(x0)=0左右侧导数的符号.回味无穷篇(作业)1.思考题极值和最值的区别与联系.