勾股定理-(2)VIP免费

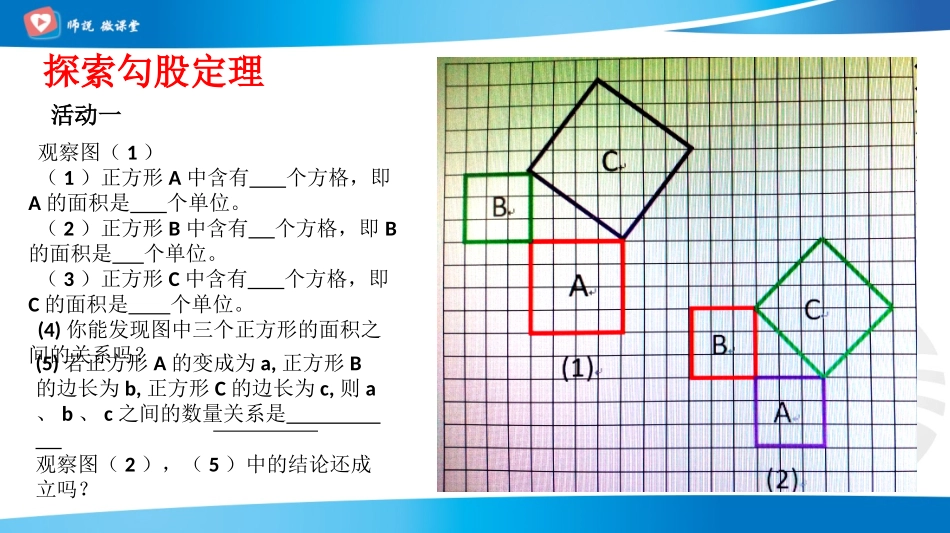
勾股定理勾股弦位桥中学栾香敬222弦股勾勾股定理简介探索勾股定理活动一观察图（1）（1）正方形A中含有个方格，即A的面积是个单位。（2）正方形B中含有个方格，即B的面积是个单位。（3）正方形C中含有个方格，即C的面积是个单位。(4)你能发现图中三个正方形的面积之间的关系吗？(5)若正方形A的变成为a,正方形B的边长为b,正方形C的边长为c,则a、b、c之间的数量关系是观察图（2），（5）中的结论还成立吗？勾股定理如果直角三角形的两直角边分别为a，b，斜边为c，那么222cba直角三角形两直角边的平方和等于斜边的平方。222弦股勾数学符号表示为：∵∠C=90º∴abcBCA勾股弦222cba验证勾股定理活动二用以下几个图形验证勾股定理abcbaccc图一图二图三学以致用222cba解：∵∠C=90º∴∵a=5,c=7∴2227c52275c∴74在RtABC△中，∠C=90º（1）已知a=5,b=7,求c的值(2)已知b=60，c=61,求a的值解：∵∠C=90º222cba∵b=60，c=61∴2226160a226061a6061606112111∴22bca22acb∴我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.1955年，希腊发行了一张邮票，图案由三个棋盘排列而成，这张邮票是纪念2500年前希腊一个学术和宗教团体——毕达哥拉斯学派,它的成立以及在文化上的贡献。勾股定理的影响：以代数的思想与概念来解决几何问题，正是“数形结合”思想的体现推动了人类对数学几何更深的探索希帕索斯根据勾股定理发现了第一个无理数,导致第一次数学危机。2（1）图a中，正方形A的面积是；图b中，正方形B的面积是。169A169144B（2）已知直角三角形的两条边长分别是6，8，则第三边的平方为ab课堂练习难点答疑（3）如图，以RtABC△的三边为直径向外做三个半圆，则它们的面积S1、S2、S3之间的数量关系是作业：必做题：课本152页习题A组3题选做题：课本153页习题B组1、2题。一样的知识不同的视角