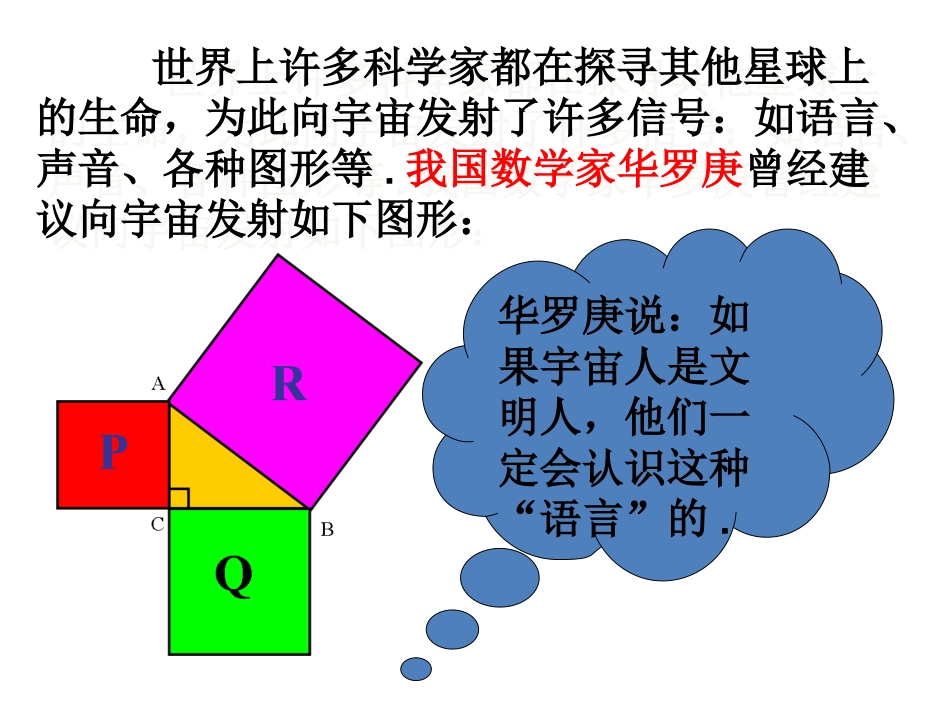
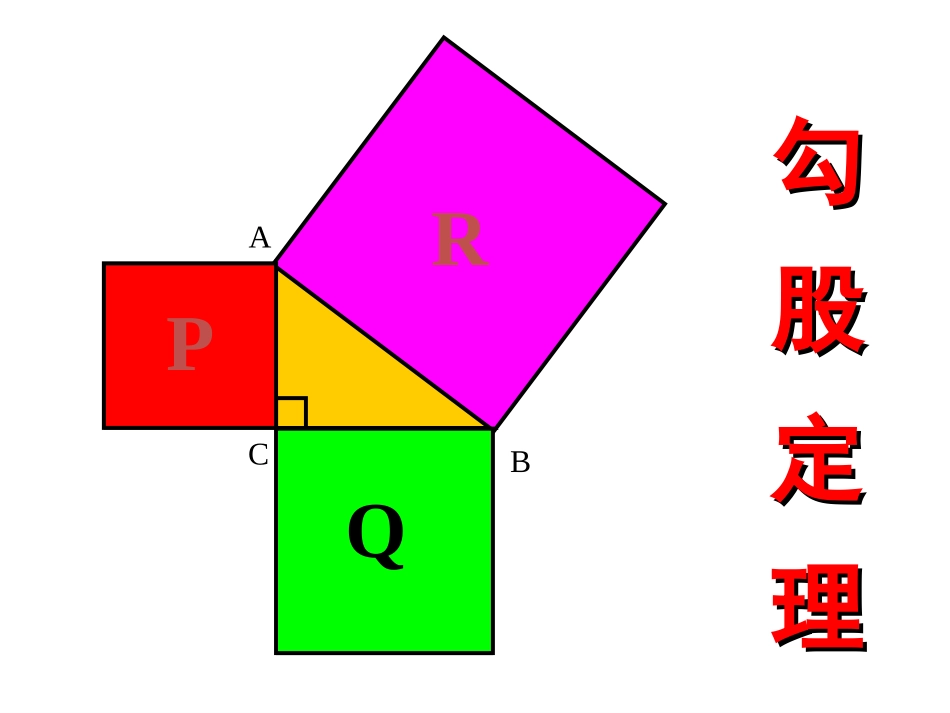
世界上许多科学家都在探寻其他星球上的生命,为此向宇宙发射了许多信号:如语言、声音、各种图形等.我国数学家华罗庚曾经建议向宇宙发射如下图形:世界上许多科学家都在探寻其他星球上的生命,为此向宇宙发射了许多信号:如语言、声音、各种图形等.我国数学家华罗庚曾经建议向宇宙发射如下图形:华罗庚说:如果宇宙人是文明人,他们一定会认识这种“语言”的.华罗庚说:如果宇宙人是文明人,他们一定会认识这种“语言”的.ABCPQR勾股定理勾股定理邮票赏邮票赏析析这是1955年希腊曾经发行的纪念一位数学家的邮票。观察这枚邮票图案小方格的个数,你有什么发现?ABCPQR实验1:将每个小正方形的面积看作1,△ABC是以格点为顶点的直角三角形,分别以三边向外作正方形。你能计算以AB为边的正方形的面积吗?SP=9SQ=16GB合作助学:ABCPQRGBPQRacbSP+SQ=SR猜想:两直角边a、b与斜边c之间的关系?a2+b2=c2CAB你能用语言叙述这一结论?acbSP+SQ=SR猜想两直角边a、b与斜边c之间的关系?a2+b2=c2CAB┏a2+b2=c2acb直角三角形两直角边的平方和等于斜边的平方.勾股定理两千多年前,古希腊有个哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯年希腊曾经发行了一枚纪念票。定理。为了纪念毕达哥拉斯学派,1955勾股世界勾股世界国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前,国家之一。早在三千多年前两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。1.已知a、b、c是三角形的三边,则a2+b2=c2.()2.在直角三角形中,两边的平方和等于第三边的平方.()3.在RtABC△中,∠A=90°,所以a2+b2=c2.()×××检测促学1.求下列图中表示边的未知数x、y、z的值.①81144xyz②③625576144169x=15y=5z=7检测促学2.求下列直角三角形中未知边的长:可用勾股定理建立方程.方法小结:8x171620x125xX=15X=12X=13①②③检测促学如图,将长为10米的梯子AC斜靠在墙上,BC长为6米。(1)求梯子上端A到墙的底端B的距离AB。(2)若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?如图,将长为10米的梯子AC斜靠在墙上,BC长为6米。(1)求梯子上端A到墙的底端B的距离AB。(2)若梯子下部C向后移动2米到C1点,那么梯子上部A向下移动了多少米?C1CBAA11062拓展导学(选用)xx10108811、如图,、如图,x=_______x=_______662、一个高3米,宽4米的大门,需在相对角的顶点间加一个加固木条,则木条的长为________3455米米检测促学253、已知:Rt△ABC中,AB=4,AC=3,则BC2的长为.43ACB43CAB或7检测促学5cmEFMEDDCCBBAA44、如图,、如图,MM、、EE、、FF均为正方形,且正方均为正方形,且正方形形MM的边长为的边长为5cm5cm检测促学回顾与思考勾股定理转化思想数形结合思想方程思想必做题:课本82页,第1、2题;选做题:查阅有关勾股定理的历史资料,了解我国古代数学家的成就.作业这是用“补”的方法ABCPQRSR=25ABCPQRSR=25这是用“割”的方法这是用“补”的方法ABCPQRSR=18这是用“割”的方法ABCPQRSR=18