2.1.2整式-多项式.1.2多项式VIP免费

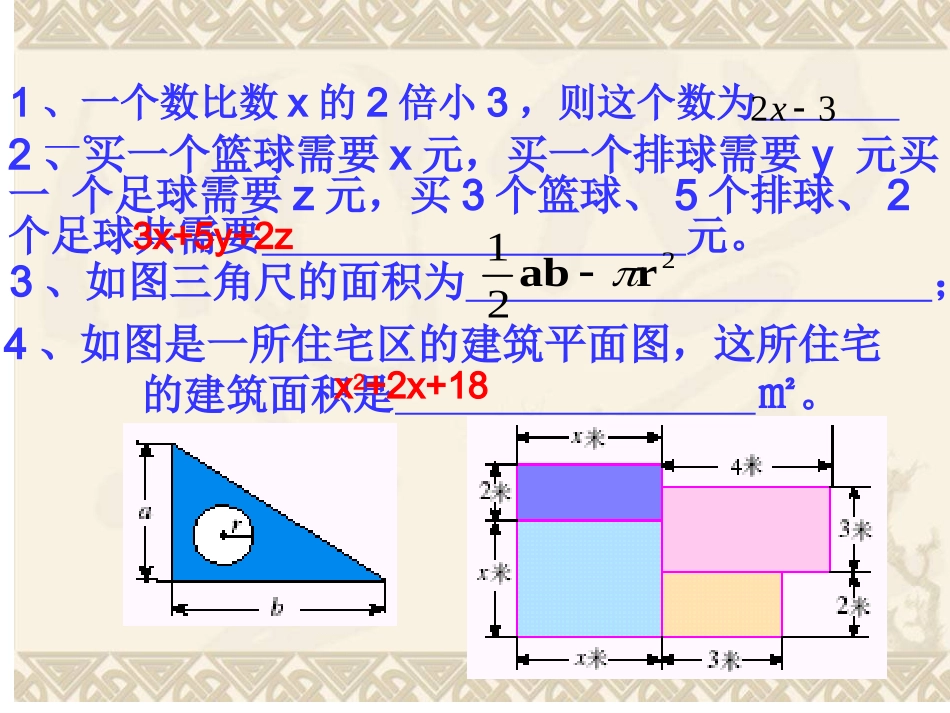
1.判断下列各式是否为单项式2.指出下列各单项式的系数与次数课前热身baxy261b5m25x23mn23xy3232xyz32、买一个篮球需要x元，买一个排球需要y元买一个足球需要z元，买3个篮球、5个排球、2个足球共需要元。1、一个数比数x的2倍小3，则这个数为。3、如图三角尺的面积为；4、如图是一所住宅区的建筑平面图，这所住宅的建筑面积是㎡。2、买一个篮球需要x元，买一个排球需要y元买一个足球需要z元，买3个篮球、5个排球、2个足球共需要元。1、一个数比数x的2倍小3，则这个数为。3、如图三角尺的面积为；4、如图是一所住宅区的建筑平面图，这所住宅的建筑面积是㎡。3x+5y+2zx2+2x+18221rab23x2x-33x+5y+2zx2+2x+181.将上面各式按和的形式读出来；2.它们有什么共同特点？几个单项式的和叫做多项式。判断：x2+xy+y，3x-2x，2+13-5，，中多项式有x2+xy+y，3x-2x，2+13-5，我思,我进步探究探究&&归归纳纳☞☞2baa观察观察&&探探究究213x213x2x-33x+5y+2zx2+2x+181.在多项式中，每个单项式叫做多项式的项。2.不含字母的项叫做常数项。3.多项式中所含单项式的个数是多项式的项数，一个多项式含有几个单项式就叫几项式。如：2x-3有两项：2x、-3常数项是-3,是二项式，，，，没有；二项式没有；二项式读读读读&&想想想想多项式多项式t-5t-53x+5y+2x2+2x+18，，，，，，读一读，想一想它们的项分别是什么，常数项分读一读，想一想它们的项分别是什么，常数项分别是什么，分别是几项式？别是什么，分别是几项式？①①t,-5;-5t,-5;-5；；二项式二项式②②3x,+5y,+2;+23x,+5y,+2;+2；；三项式三项式④④xx22,+2x,+,+2x,+18;1818;18；；三项式三项式注意：注意：多项式的每一多项式的每一项都项都包含它前包含它前面的符号面的符号。。2r③12ab想想想想&&讲讲讲讲多项式多项式a2+a3b+6，它的项分别是它的项分别是a2、、a3b、、6，，___是二次项，是二次项，___是四次项，___是常数项．其中次数最高项的次数是（）。其中次数最高项的次数是（）。44多项式中多项式中次数最高项的次数次数最高项的次数叫做叫做练一练a2a3b6多项式的次数多项式的次数x2+2x+18的次数是；t-5的次数是3x+5y+2的次数；的次数是ab3.1421想想想想&&讲讲讲讲多项式多项式a2+a3b+6，它的项分别是它的项分别是a2、、a3b、、6，，___是二次项，是二次项，___是四次项，___是常数项．其中次数最高项的次数是（）。其中次数最高项的次数是（）。44多项式中多项式中次数最高项的次数次数最高项的次数叫做叫做练一练a2a3b6多项式的次数多项式的次数x2+2x+18是次项式；t-5是次项式3x+5y+2是次项式；是次项式ab3.1421多项式的名称：次数最高项的次数是几就是几次式，含有几项就是几项式，称为几次几项式练一练2x+12x+13322、、是是_____式，它的项分别是的项分别是_________，，它的常数项是（它的常数项是（），它是，它是_____次多次多项式，也可以说是项式，也可以说是次次项式。项式。多项、131111332x一一二二1、下列说法错误的是（）A.是三次五项式B.是二次四项式C.的常数项是D.是一次四项式23231xyxyxy8356xyxy23231xxyxy231xyxy1注意：有些多项式写成分数的形式规定：单项式与多项式统称为整式。判断：下列式子是否为整式整式：234x整式单项式多项式2xy1x21xy2234x221xy2xy填表：整式系数，，，次数项数练一练15ab224ab235xy243x42242aabb15214335324114221143单项式多项式次数:所有字母的指数的和。系数：单项式中的数字因数。项：式中的每个单项式叫多项式的项。（其中不含字母的项叫做常数项）次数：多项式中次数最高的项的次数。整式项数：式中所含单项式的个数名称