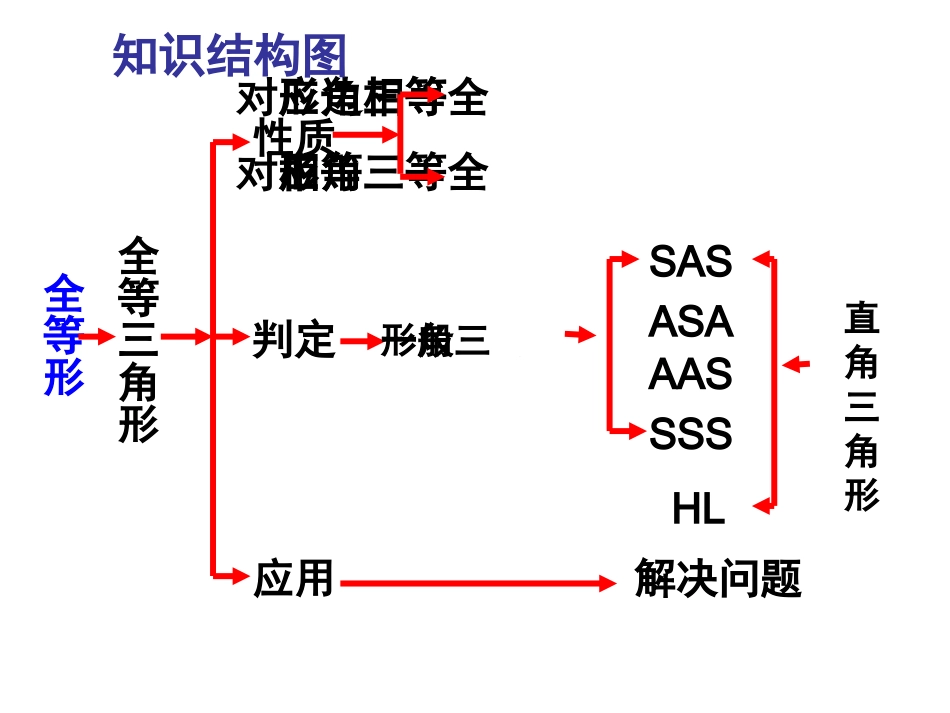
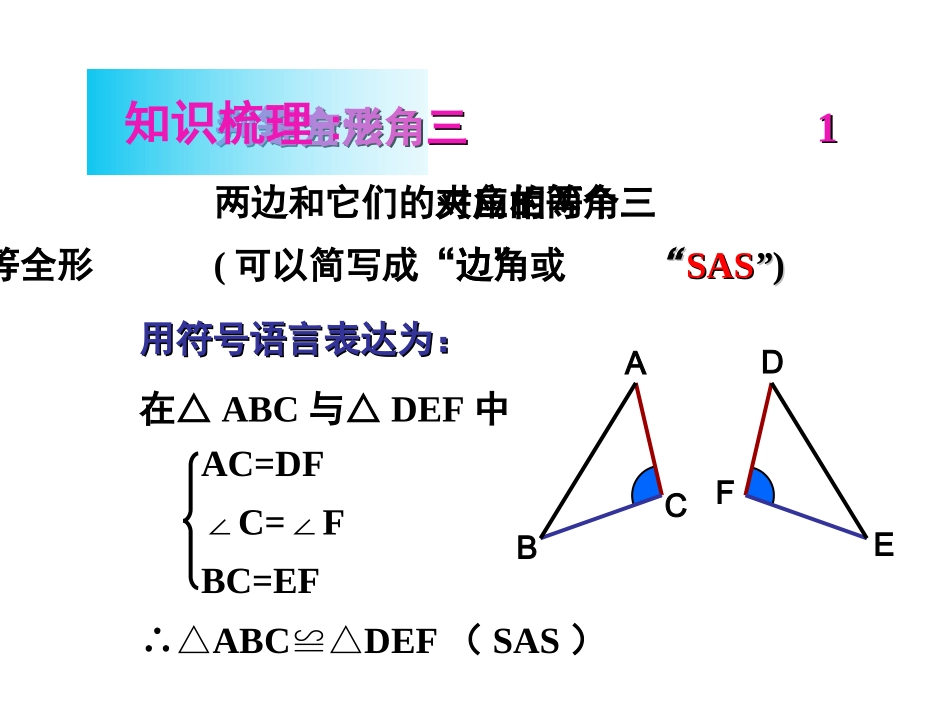
三角形全等的判定复习课全等形全等三角形性质判定应用HL全等三角形对应边相等全等三角形对应角相等解决问题SASASAAASSSS一般三角形直角三角形知识结构图三角形全等判定方法三角形全等判定方法11用符号语言表达为:用符号语言表达为:在△ABC与△DEF中∴△ABCDEF≌△(SAS)两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或““SASSAS””))知识梳理:FEDCBAAC=DF∠C=F∠BC=EF∠A=D∠(已知)AB=DE(已知)∠B=E∠(已知)在△ABC和△DEF中∴△ABCDEF△(ASA)有两角和它们夹边对应相等的两个三角有两角和它们夹边对应相等的两个三角形全等形全等((可以简写成“角边角”或“可以简写成“角边角”或“ASAASA””)。)。用符号语言表达为:用符号语言表达为:FEDCBA三角形全等判定方法三角形全等判定方法22知识梳理:知识梳理:三角形全等判定方法三角形全等判定方法33有两角和其中一个角的对边对应相等的两有两角和其中一个角的对边对应相等的两个三角形全等个三角形全等((可以简写成“角角可以简写成“角角边”或“边”或“AASAAS””用符号语言表达为:用符号语言表达为:CBAFED三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。ABCDEF在△ABC和△DEF中∴△ABCDEF≌△(SSS)AB=DEBC=EFCA=FD用符号语言表达为:用符号语言表达为:三角形全等判定方法三角形全等判定方法44知识梳理:知识梳理:DCBAABDABDABCSSASSA不不能判定全能判定全等等ABCABCA′B′C′知识梳理:直角三角形全等判定:直角三角形全等判定:HLHL二、几种常见全等三角形基本图形二、几种常见全等三角形基本图形FEDCBAFEDCBAFEDCBA平移EDCBAEDCBA旋转如:课本P16第10题课本P26第3题EDCBADCBADCBAEDCBA翻折如:课本P10第2题课本P13第2题课本P15第3题1、证明两个三角形全等例例11:如图:如图,,点点BB在在AEAE上上,CAB=DAB,∠∠,CAB=DAB,∠∠要使要使ΔABCΔABD,≌ΔABCΔABD,≌可补充的一可补充的一个条件是个条件是..EDCBA分析:现在我们已知分析:现在我们已知AA→CAB=DAB∠∠→CAB=DAB∠∠①①用用SAS,SAS,需要补充条需要补充条件件AD=AC,AD=AC,②②用用ASA,ASA,需要补充条需要补充条件件∠∠CBA=DBA,∠CBA=DBA,∠③③用用AAS,AAS,需要补充条需要补充条件件∠∠C=D,∠C=D,∠④④此外此外,,补充条件补充条件∠∠CBE=DBE∠CBE=DBE∠也可以也可以(?)(?)SASSASASAASAAASAASSS→AB=AB(→AB=AB(公共边公共边).).AD=ACAD=AC∠∠CBA=DBA∠CBA=DBA∠∠∠C=D∠C=D∠∠∠CBE=DBE∠CBE=DBE∠例2已知:如图,AB=AC,AD=AE,∠1=∠3,那么∠E=∠D吗?为什么?1.2、证明两个角相等 BE=EB(BE=EB(公共边公共边))又 又 ACDB(∥ACDB(∥已知已知))DBE=CEB(∠∠DBE=CEB(∠∠两直线平两直线平行行,,内错角相等内错角相等))例例3:3:如图如图,ACDB,AC=2DB,E∥,ACDB,AC=2DB,E∥是是ACAC的中点的中点,,求证求证:BC=DE:BC=DE证明证明:AC=2DB,AE=EC :AC=2DB,AE=EC ((已知已知)DB=EC∴)DB=EC∴EDCBADB=ECDB=ECBE=EBBE=EB∴∴ΔDBEΔCEB(SAS)≌∴ΔDBEΔCEB(SAS)≌∴BC=DE(BC=DE(全等三角形的对全等三角形的对应边相等应边相等))3、证明两条线段相等练习:已知:∠ACB=∠ADB=900,AC=AD,P是AB上任意一点,求证:CP=DPCABDP例例4(20074(2007金华金华):):如图如图,A,E,B,D,A,E,B,D在同一直线上在同一直线上,,AB=DE,AC=DF,ACDF,∥AB=DE,AC=DF,ACDF,∥在在ΔABCΔABC和和ΔDEF,ΔDEF,(1)(1)求证求证:ΔABCΔDEF;≌:ΔABCΔDEF;≌((2)2)你还可以得到的结论是你还可以得到的结论是..((写出一个写出一个,,不再添加其他线段不再添加其他线段,,不不再表注或使用其他字母再表注或使用其他字母))FEDCBA(1)(1)证明证明:ACDF( ∥:ACDF( ∥已知已知))A=D(∴∠∠A=D(∴∠∠两直线平两直线平行行,,内错角相等内错角相等))AB=DE(AB=DE(已知已知))A=D(∠∠A=D(∠∠已已证证)AC=DF)AC=DF((已知已知))∴∴ΔABCΔDEF(SAS)≌ΔABCΔDEF(SAS)≌在在ΔABCΔABC和和ΔDEFΔDEF中中综合题:FEDCBA((22)解)解::根据”全等三角形的对应边根据”全等三角形的对应边((角角))相等”可知相等”可知::②∠②∠C=F,∠C=F,∠③∠③∠ABC=D...