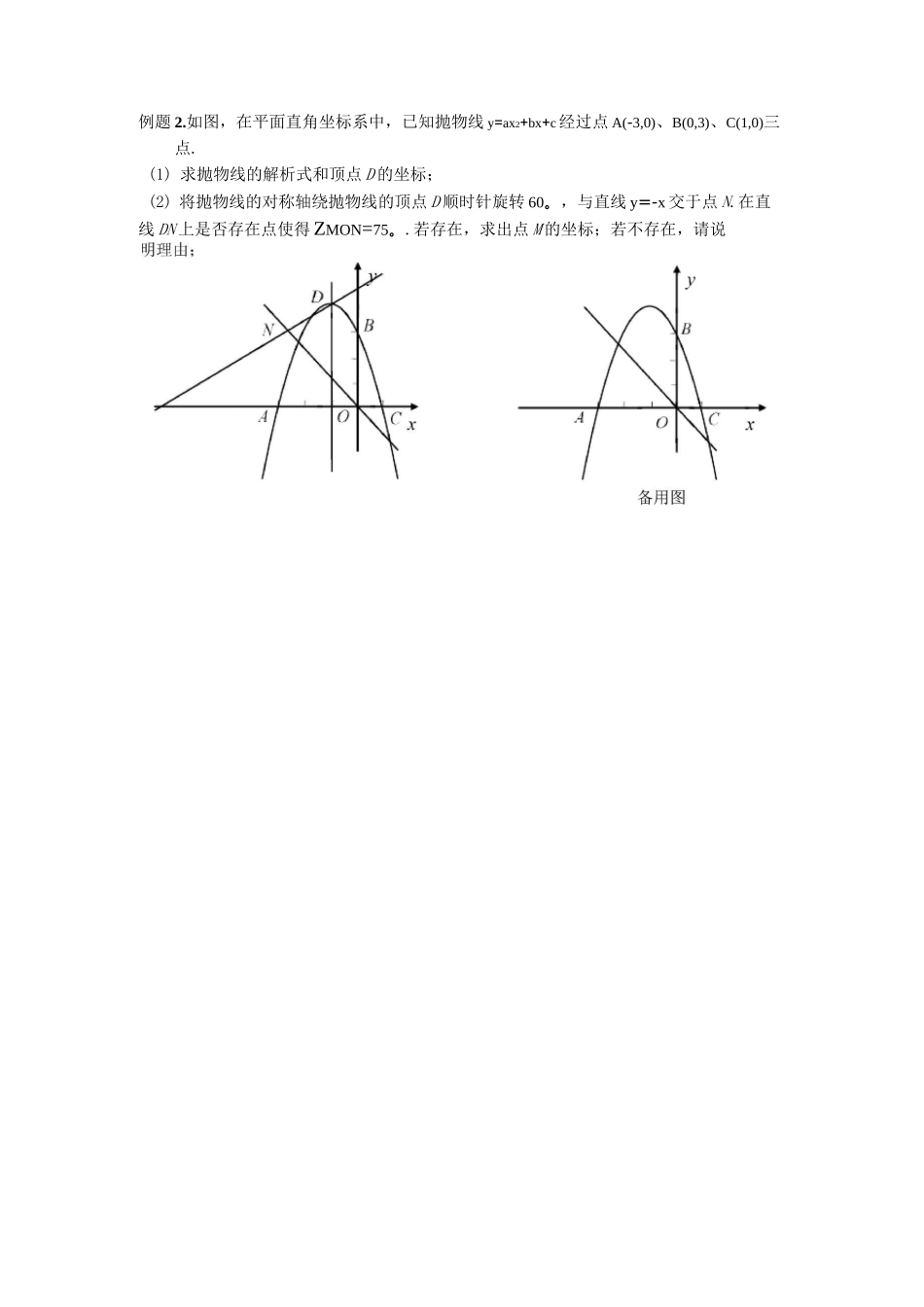
2020中考数学压轴专题角度存在性和角度关系问题1.角度的存在性问题角度的存在性问题分为特殊角和非特殊角的存在性问题,在考试中主要以特殊角的存在性问题为主,特殊角通常包括30。、45。、60。、90。等.几何法:利用(特殊)角度构造直角三角形,从边长比例关系进行求解.2.角度关系的存在性问题角度关系的问题一般指两角或多角的和差倍分或大小关系的问题几何法:构造相似或全等三角形进行求解.解析法:利用三角函数值进行求解.和差关系(ZA+ZC=ZABD)等量关系大小关系D-「亠C转化为三角形全等或相似找临界值,即找等量关系{例题精练模块一角度的存在性问题例题1.如图,抛物线y=ax2+bx-4a经过A(-1,0),C(0,4)两点,与x轴交于另一点B.(1)求抛物线的解析式;(2)已知点D(m,m+1)在第一象限的抛物线上,连接BD,在抛物线上是否存在点P使得ZDBP=45。?若存在,请求出点P的坐标;不存在,说明理由.例题2.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+c经过点A(-3,0)、B(0,3)、C(1,0)三点.(1)求抛物线的解析式和顶点D的坐标;(2)将抛物线的对称轴绕抛物线的顶点D顺时针旋转60。,与直线y=-x交于点N.在直线DN上是否存在点使得ZMON=75。.若存在,求出点M的坐标;若不存在,请说模块二角度关系的存在性问题1例题3.如图,在平面直角坐标系x^y中,二次函数y二-X2+bx+c的图象经过点A(-3,6),2并与x轴交于点B(-1,0)和点C,顶点为P.(1)求二次函数的解析式;(2)设D为线段OC上的一点,若ZDPC=ZBAC,求点D的坐标.例题4.如图,已知抛物线y=ax2+bx+c的对称轴为直线弋=乜,且与x轴交于A、两点.与尹轴交于点C.其中A(1,0),C(0,-3).(1)求抛物线的解析式;(2)若点P在抛物线上运动(点P异于点A),3例题5.如图,已知抛物线y=(3-m)x2+2(m-3)x+4m-m2的顶点A在双曲线y=上,直x线y=mx+b经过点A,与y轴交于点5与x轴交于点C.(1)确定直线AB的解析式•(2)将直线AB绕点O顺时针旋转90。,与x轴交于点D,与y轴交于点E,求sinZBDE的值.(3)过点B作x轴的平行线与双曲线交于点G,点M在直线BG上,且到抛物线的对称轴的距离为6.设点N在直线BG上,请你直接写出使得ZAMB+ZANB=45。的点N的坐标.例题6.抛物线y=(x-3)(x+1)与x轴交于A,两点(点A在点B左侧),与尹轴交于点C,点D为顶点.(1,求点B及点D的坐标;(2)连结BD,CD,抛物线的对称轴与x轴交于点E.①若线段BD上一点P,使ZDCP=ZBDE,求点P的坐标;②若抛物线上一点M,作MN丄CD,交直线CD于点N,使ZCMN=ZBDE,求点M的坐标.备备用图04果后巩固练习1练1.如图直线y=-x+m与抛物线y=-x2+bx+c交于C、D两点,其中点C在尹轴上,点2(5AD的坐标为3,-,点P是y轴右侧的抛物线上一动点,过点P作PE丄x轴于点E,k2丿交CD于点F.(1)求一次函数和抛物线的解析式.(2)若点P的横坐标为/,当t为何值时,四边形OCPF是平行四边形?请说明理由.(3)在CD上方是否存在点P,使ZPCF=45。,若存在,求出相应的点P的坐标,若不存练2.如图,在平面直角坐标系xOy中,以直线x=1为对称轴的抛物线y=ax2+bx+c与x轴(3\从左至右依次交于A,B两点,与y轴交于点C,且AB=4,点D2,-在抛物线上,k2丿直线l是一次函数y=kx-2(k丰0)的图象.(1)求抛物线的解析式;(2)如果直线l平分四边形OBDC的面积,求k的值;(3)将抛物线作适当平移,求解与探究下列问题;①若将抛物线y=ax2+bx+c向下平移m个单位长度后,恰与第(2)问中的直线l有且只有一个公共点,求m的值;②把抛物线y=ax2+bx+c向左平移1个单位,再向下平移2个单位,所得抛物线与直线I交于M,N两点,请在备用图中画出草图,并探究:在y轴正半轴上是否存在一定点P,使得无论k取何值,ZMPN总被y轴平分?若存在,求出P点坐标;若不存在,请说明理由.备用图422练3.如图3-1,已知直线y=kx与抛物线y=-方x2+-^交于点(3,6).(1)求直线y=kx的解析式和线段OA的长度.(2)点P为抛物线第一象限内的动点,过点P作直线PM,交x轴于点M(点M、O不重合),交直线OA于点0,再过点Q作直线PM的垂线,交尹轴于点N.试探究:线段QM与线段NQ的长度之比是否为定值?如果是,求出这个定值;如果不是,说明理由.(3)如图3-2,若点B为抛物线上对称轴右侧的点,点E在线段OA上(与点O.A不重合),点D(m,0)是x轴正半轴上的动点,且满足ZBAE=ZBED=ZAOD.继续探究:m在什么范围时,符合条件的E点的个数分别是1个、2个?