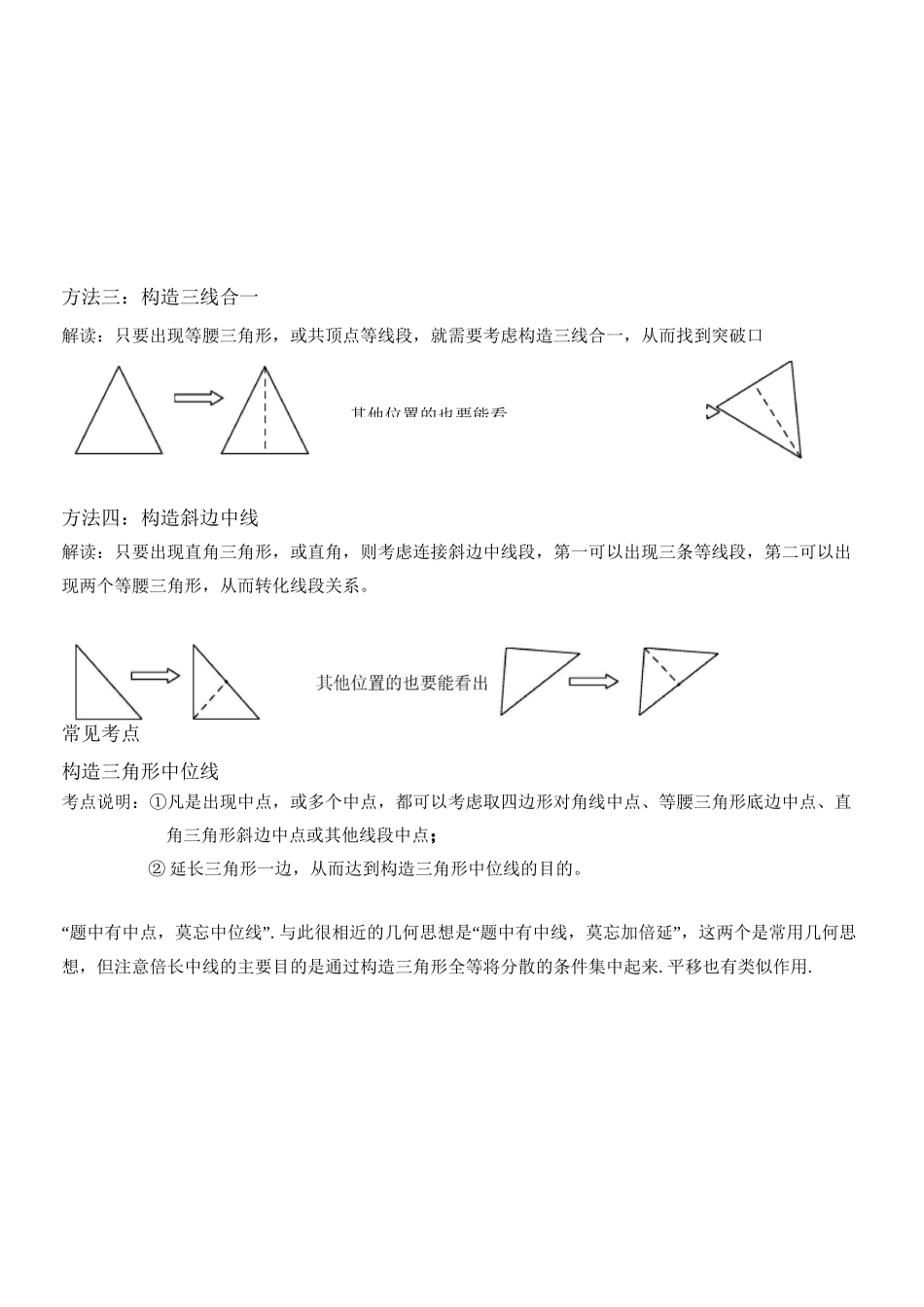
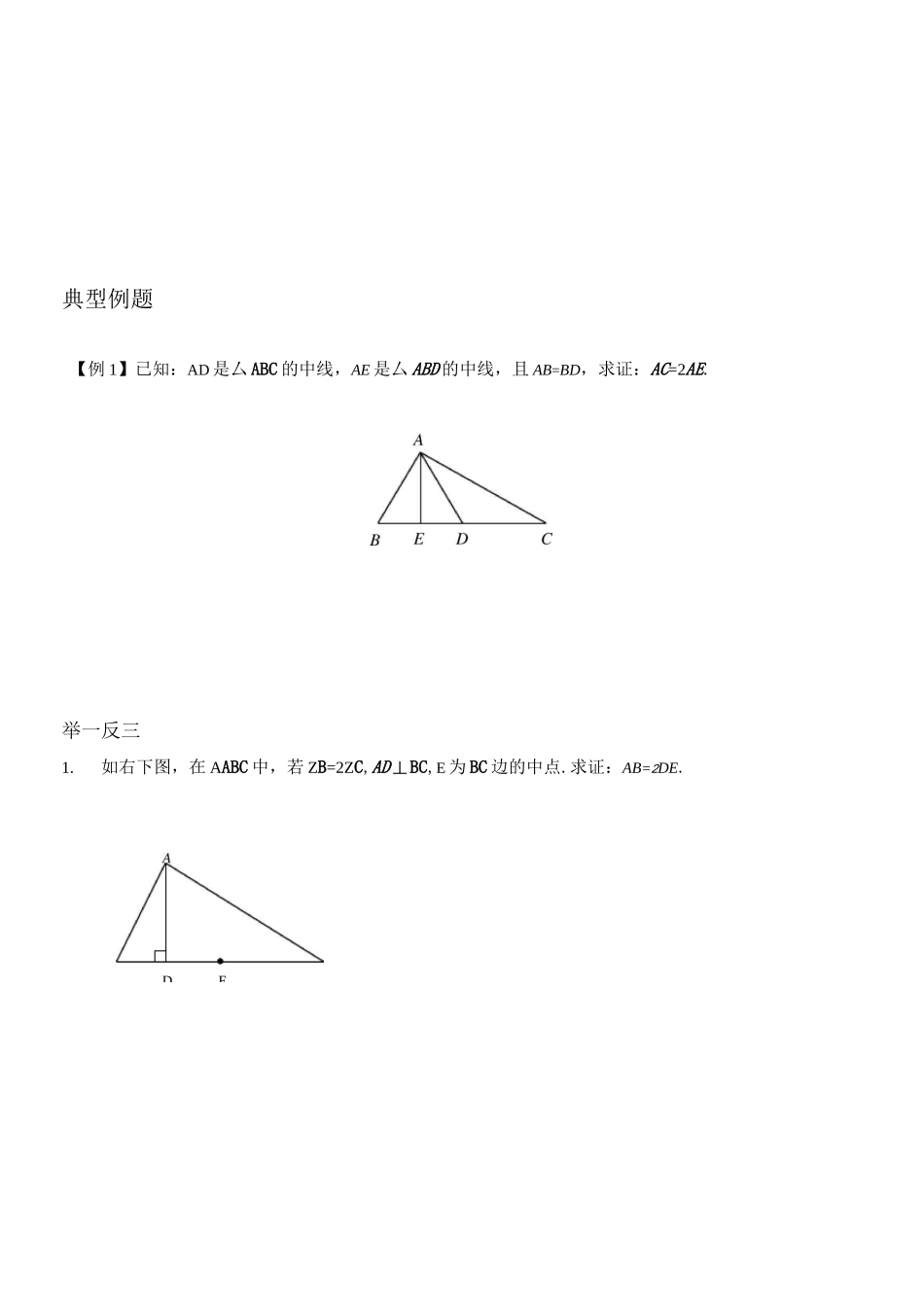
三角形中位线中的常见辅助线知识梳理知识点一中点一、与中点有关的概念三角形中线的定义:三角形顶点和对边中点的连线等腰三角形底边的中线三线合一(底边的中线、顶角的角平分线、底边的高重合)三角形中位线定义:连结三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线平行于第三边并且等于它的一半.中位线判定定理:经过三角形一边中点且平行于另一边的直线必平分第三边.直角三角形斜边中线:直角三角形斜边中线等于斜边一半斜边中线判定:若三角性一边上的中线等于该边的一半,则这个三角形是直角三角形二、与中点有关的辅助线方法一:倍长中线解读:凡是出现中线或类似中线的线段,都可以考虑倍长中线,倍长中线的目的可以旋转等长度的线段,从而达到将条件进行转化的目的。V方法二:构造中位线解读:凡是出现中点,或多个中点,都可以考虑取另一边中点,或延长三角形一边,从而达到构造三角形中位线的目的。其他位置的也要能看方法三:构造三线合一解读:只要出现等腰三角形,或共顶点等线段,就需要考虑构造三线合一,从而找到突破口方法四:构造斜边中线解读:只要出现直角三角形,或直角,则考虑连接斜边中线段,第一可以出现三条等线段,第二可以出现两个等腰三角形,从而转化线段关系。常见考点构造三角形中位线考点说明:①凡是出现中点,或多个中点,都可以考虑取四边形对角线中点、等腰三角形底边中点、直角三角形斜边中点或其他线段中点;②延长三角形一边,从而达到构造三角形中位线的目的。“题中有中点,莫忘中位线”.与此很相近的几何思想是“题中有中线,莫忘加倍延”,这两个是常用几何思想,但注意倍长中线的主要目的是通过构造三角形全等将分散的条件集中起来.平移也有类似作用.DE典型例题【例1】已知:AD是厶ABC的中线,AE是厶ABD的中线,且AB=BD,求证:AC=2AE.举一反三1.如右下图,在AABC中,若ZB=2ZC,AD丄BC,E为BC边的中点.求证:AB=2DE.2.在AABC中,ZACB=90。,AC=2BC,以BC为底作等腰直角ABCD,E是CD的中点,求证:AE丄EB且AE=BE.【例2】已知四边形ABCD的对角线AC=BD,E、F分别是AD、BC的中点,连结EF分别交AC、BD于M、N,求证:ZAMN=ZBNM.举一反三1.已知四边形ABCD中,ACZGNM.F2.已知:在AABC中,BC>AC,动点D绕AABC的顶点A逆时针旋转,且AD=BC,连结DC.过AB、DC的中点E、F作直线,直线EF与直线AD、BC分别相交于点M、N.(1)如图1,当点D旋转到BC的延长线上时,点N恰好与点F重合,取AC的中点H,连结HE、HF,求证:ZAMF=ZBNE(2)当点D旋转到图2中的位置时,ZAMF与ZBNE有何数量关系?请证明.【例3】如图,在五边形ABCDE中,ZABC=ZAED=90。,ZBAC=ZEAD,F为CD的中点.求证:BF=EF.举一反三1.如图所示,在三角形ABC中,D为AB的中点,分别延长CA、CB到点E、F,使DE=DF•过E、F分别作直线CA、CB的垂线,相交于点P,设线段PA、PB的中点分别为M、N.求证:(1)ADEM9AFDN;(2)ZPAE=ZPBF.r3.已知:在AABC中,分别以AB、AC为斜边作等腰直角三角形ABM,和CAN,P是边BC的中点.求证:PM=PN4.如图所示,已知AABD和AACE都是直角三角形,且ZABD=ZACE=90°,连接DE,设M为DE的中占八、、•(1)求证MB=MC.(2)设ZBAD=ZCAE,固定RtAABD,让RtAACE移至图示位置,此时MB=MC是否成立?请证明你的结论.5.在厶ABC中,AB=AC,分别以AB和AC为斜边,向厶ABC的外侧作等腰直角三角形,M是BC边中点中点,连接MD和ME(1)如图1所示,若AB=AC,则MD和ME的数量关系是(2)如图2所示,若AB^AC其他条件不变,则MD和ME具有怎样的数量和位置关系?请给出证明过程;(3)在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,M是BC的中点,连接MD和ME,请在图3中补全图形,并直接判断△MED的形状.【例4】以AABC的两边AB、AC为腰分别向外作等腰RtAABD和等腰RtAACE,ZBAD=ZCAE=90。.连接DE,M、N分别是BC、DE的中点.探究:AM与DE的位置关系及数量关系.(1)____________________________________________________________如图①当AABC为直角三角形时,AM与DE的位置关系是;线段AM与DE的数量关系是(2)...