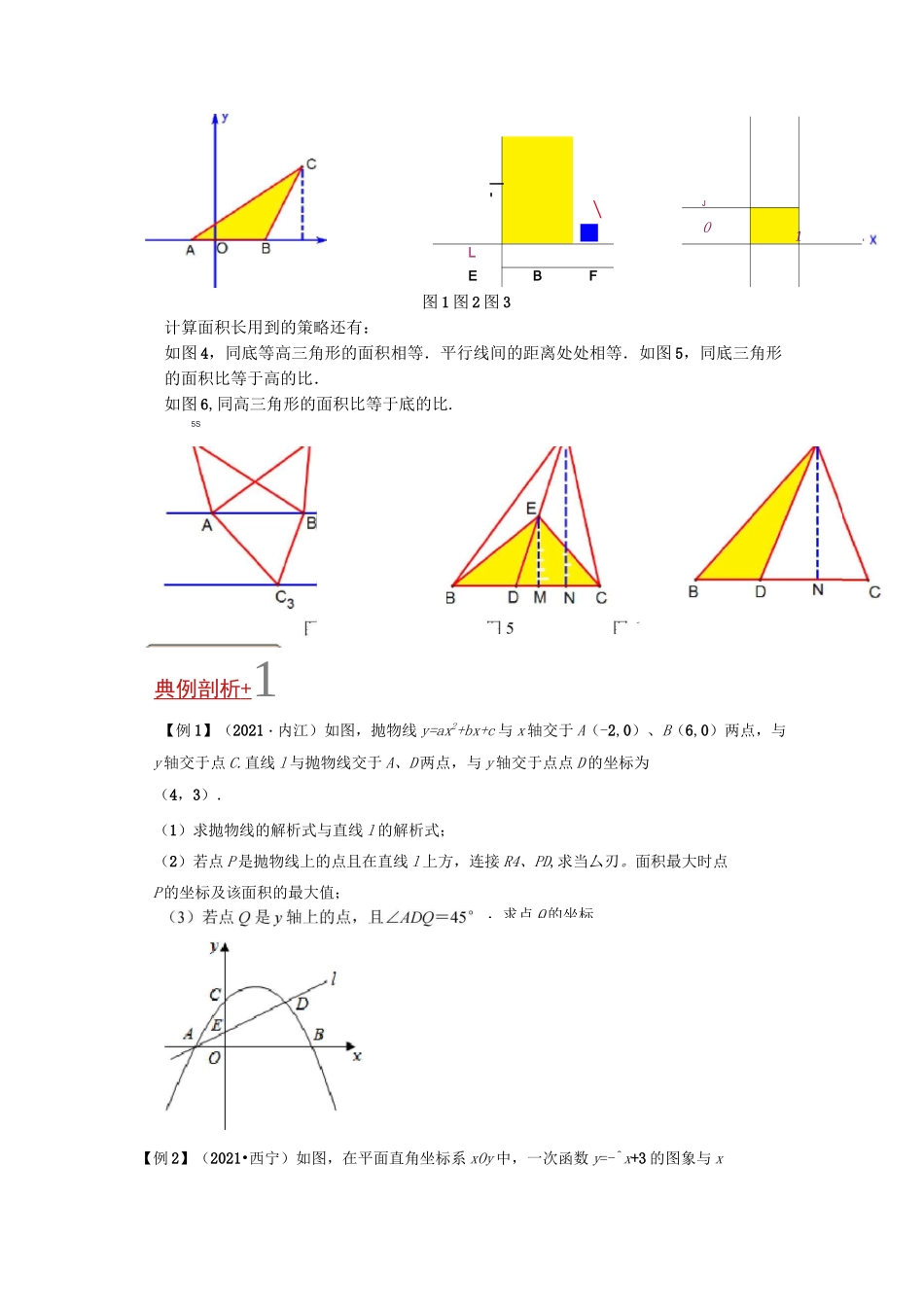
专题5二次函数与面挑战2022年中考数学压轴题之学霸秘笈大揭秘专题5二次函数与面积最值定值问题好题快递若法综述,J面积是平面几何中一个重要的概念,关联着平面图形中的重要元素边与角,由动点而生成的面积问题,是抛物线与直线形结合的觉形式,常见的面积问题有规则的图形的面积(如直角三角形、平行四边形、菱形、矩形的面积计算问题)以及不规则的图形的面积计算,解决不规则的图形的面积问题是中考压轴题常考的题型,此类问题计算量较大。有时也要根据题目的动点问题产生解的不确定性或多样性。解决这类问题常用到以下与面积相关的知识:图形的割补、等积变形、等比转化等数学方法.面积的存在性问题常见的题型和解题策略有两类:一是先根据几何法确定存在性,再列方程求解,后检验方程的根.二是先假设关系存在,再列方程,后根据方程的解验证假设是否正确.方法揭私解决动点产生的面积问题,常用到的知识和方法,如下:如图1,如果三角形的某一条边与坐标轴平行,计算这样“规则”的三角形的面积,直接用面积公式.如图2,图3,三角形的三条边没有与坐标轴平行的,计算这样“不规则”的三角形的面积,用“割”或“补”的方法.輕二题组题组题组题组—'\■LEBFJ10图1图2图3计算面积长用到的策略还有:如图4,同底等高三角形的面积相等.平行线间的距离处处相等.如图5,同底三角形的面积比等于高的比.如图6,同高三角形的面积比等于底的比.典例剖析+1【例1】(2021・内江)如图,抛物线y=ax2+bx+c与x轴交于A(-2,0)、B(6,0)两点,与y轴交于点C.直线l与抛物线交于A、D两点,与y轴交于点点D的坐标为(4,3).(1)求抛物线的解析式与直线l的解析式;(2)若点P是抛物线上的点且在直线l上方,连接R4、PD,求当厶刃。面积最大时点P的坐标及该面积的最大值;【例2】(2021•西宁)如图,在平面直角坐标系xOy中,一次函数y=-^x+3的图象与x5S,求点Q的坐标.轴交于点A,与尹轴交于点b点C的坐标为(-2,0),抛物线经过A,B,C三点.(1)求抛物线的解析式;(2)直线AD与y轴负半轴交于点D,且ZBAO=ZDAO,求证:OB=OD;(3)在(2)的条件下,若直线AD与抛物线的对称轴l交于点连接BE,在第一象限内的抛物线上是否存在一点F,使四边形BEAP的面积最大?若存在,请求出点P的坐标及四边形BEAP面积的最大值;若不存在,请说明理由.【例3】(2021・贵港)如图,已知抛物线y=ax2+bx+c与x轴相交于A(-3,0),B两点,与y轴相交于点C(0,2),对称轴是直线x=-1,连接AC.(1)求该抛物线的表达式;(2)若过点B的直线l与抛物线相交于另一点D,当ZABD=ZBAC时,求直线l的表达式;(3)在(2)的条件下,当点D在x轴下方时,连接AD,此时在y轴左侧的抛物线上存2在点P,使S川=S^ABD•请直接写出所有符合条件的点P的坐标.【例4】(2021•襄阳)如图,直线y=^x+1与x,y轴分别交于点B,A,顶点为P的抛物线y=ax2-2ax+c过点A.(1)求出点A,B的坐标及c的值;(2)若函数y=ax2-2ax+c在3WxW4时有最大值为a+2,求a的值;(3)连接AP,过点A作AP的垂线交x轴于点M设的面积为S.①直接写出S关于Q的函数关系式及Q的取值范围;②结合S与a的函数图象,直接写出S>时a的取值范围.■5满分训练『[题组一】1.(2021•沈河区二模)如图,在直角坐标系xOy中,抛物线y=ax2+bx+2(aMO)与x轴交于点力(-1,0)和B(4,0),与y轴交于点C,点P是抛物线上的动点(不与点A,B,C重合).(1)求抛物线的解析式;(2)当点P在第一象限时,设AACP的面积为S1,^ABP的面积为S2,当S1=S2时,求点P的坐标;(3)过点O作直线l〃BC,点Q是直线l上的动点,当BQ丄PQ,且ZBPQ=ZCAB时,请直接写出点P的坐标.连接AF、BF(如图2).设△ADF、△ABF.△BEF的面积分别为»、S2、S3,是否存在常数t,使S22=fS1S3?若存在,求出t的值;若不存在,请说明理由.2(2021•泰兴市模拟)抛物线y=ax2+c的顶点为C(0,1),与直线y=kx+3(k为常数)相交于A(x1,y1),B(x2,y2)两点.当k=0时,点B的横坐标恰好为2(如图1).(1)求a、c的值;(2)当k=0时,若点P是抛物线上异于A、C的一点,且满足2PC2=AB2+2AP2,试判断厶PAC的形状,并说明理由;(3)若直线y=-1交y轴于点F,过点A、B分别作该直线的垂线,垂足分别为D、E,Sis\23.(2021•雁塔区校级模拟)如图,抛物线C1的图象...