中国经济增长问题初探三分析VIP免费

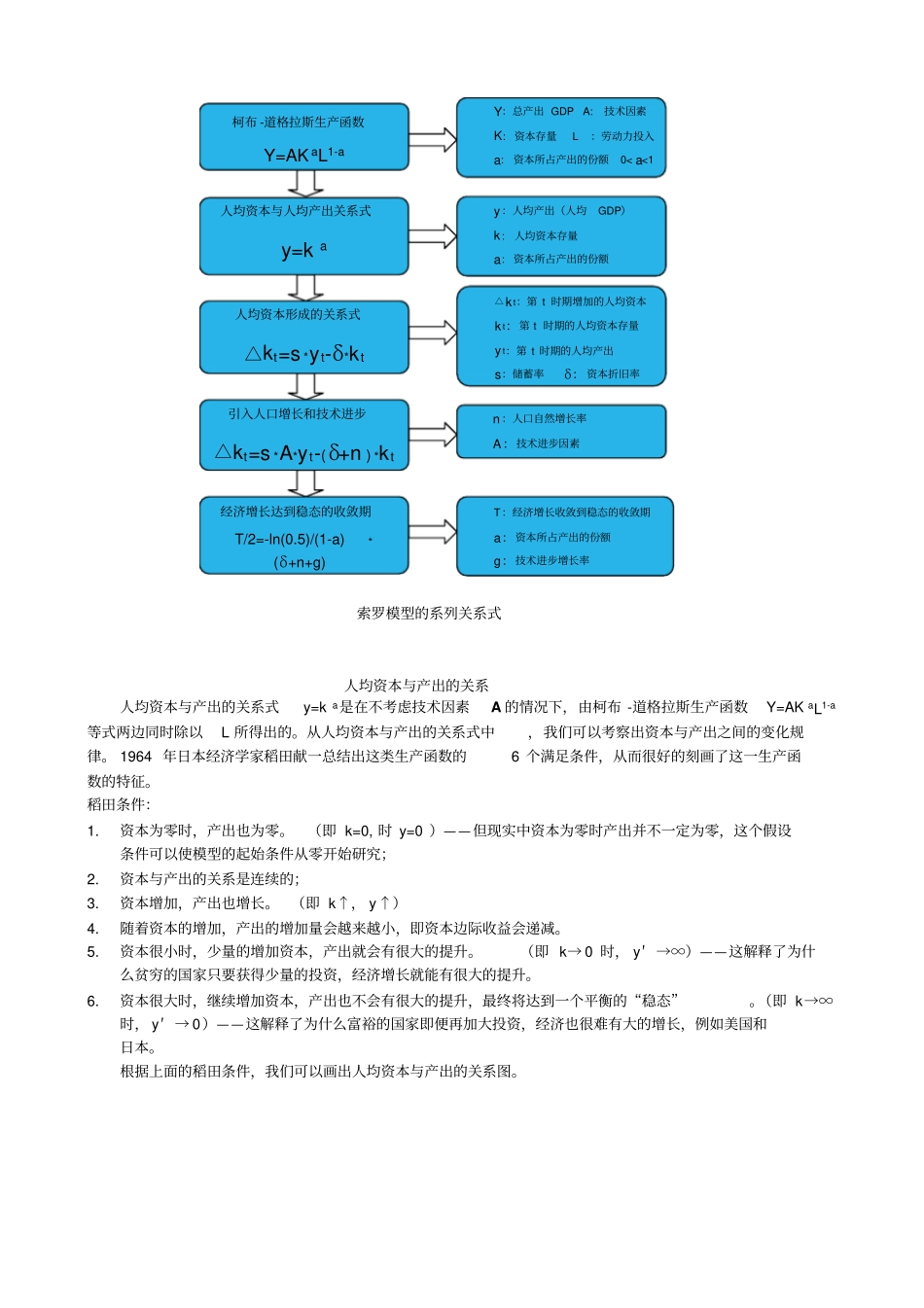
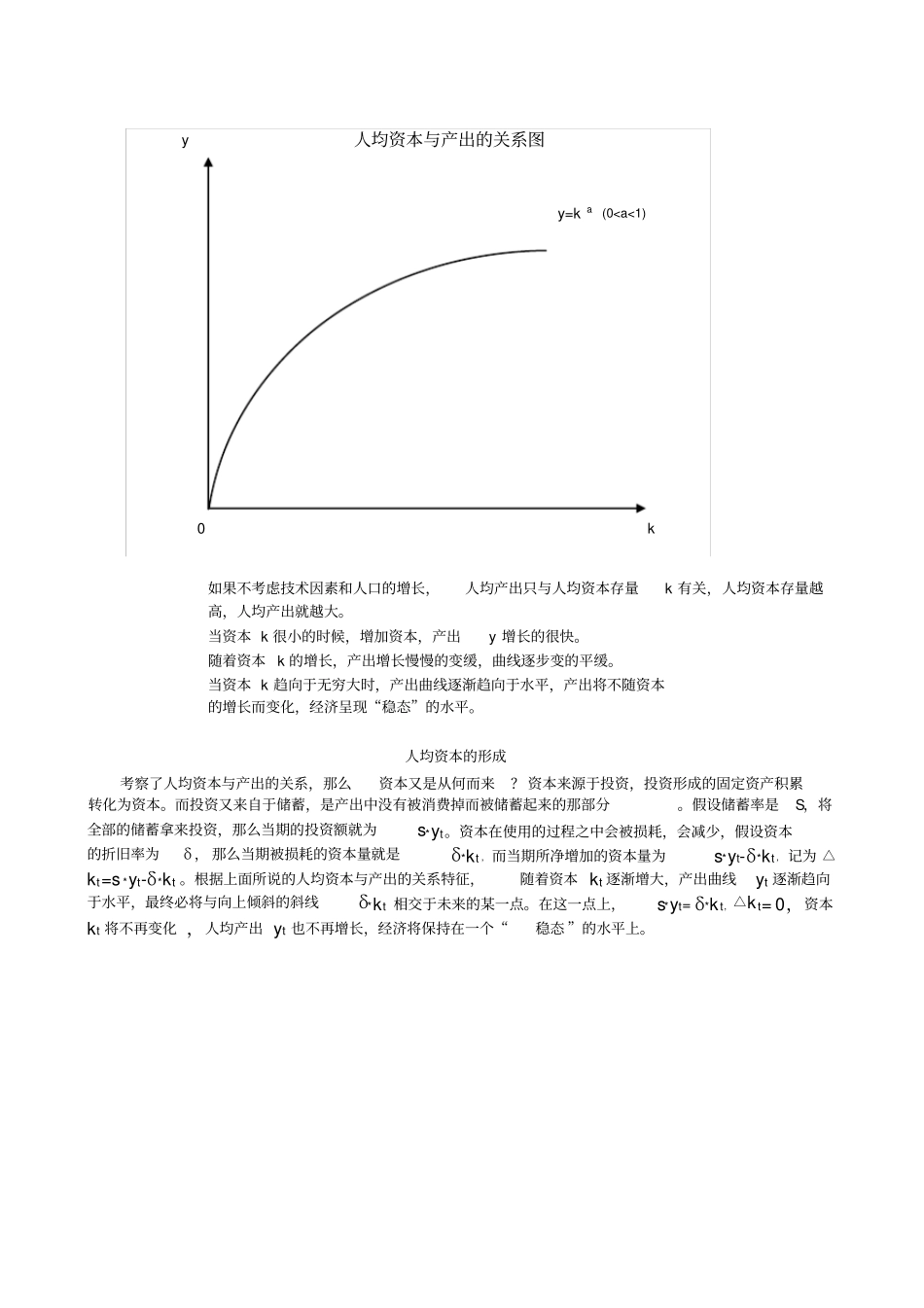
中国经济增长问题初探（三）上篇文章我们利用柯布-道格拉斯生产函数，从增长计量的角度对中国经济增长放缓的因素进行了测量。得出的结论是中国经济增长放缓的原因不在于投资，也不在于劳动力，而在于技术因素的下降。但是这个结论只是我们从数据测量的角度观察到的一个“事实”，而并非从逻辑关系推导出的理论结果。本篇文章将进一步剖析生产函数各要素之间变化的逻辑关系，探讨中国经济增长放缓的更为深层次的原因。引入索罗模型为了进一步研究生产函数各要素之间更为深层次的逻辑关系，就需要引入一个新的经济模型——“索罗模型”。“索罗模型”是美国麻省理工（MIT）的教授罗伯特·索罗在1956年为了研究经济均衡增长路径的问题而创造的，该模型创造后被广泛应用于经济增长的研究，索罗教授也并由此获得了1987年诺贝尔经济学奖。索罗模型的主要思路索罗模型的系列关系式通过对上面索罗模型主要思路的梳理，我们可以得出索罗模型的一系列的关系式。这些关系式从数理上展示了资本与产出、储蓄与投资、劳动和技术的增长与资本之间的逻辑变化关系，从而完整的表明了经济增长的最终发展方向以及推动经济发展的最终的因素。柯布-道格拉斯生产函数假定技术和劳动保持不变，单独考察资本和产出之间的变化关系——发现资本与产出之间的稻田条件特性。考察资本的积累，引入储蓄率和折旧率，建立资本增量和产出、储蓄率、折旧率之间的关系式——发现资本积累的稳态特征。引入人口增长和技术进步，在人均资本保持不变的情况下，人均产出和总产出却能够以技术进步的速率增长，从而表明技术进步是一个经济长期持续增长的源泉。根据资本积累的稳态特征，利用半衰期公式测算经济增长达到稳态的收敛期，给出经济发展的时间窗口。索罗模型的系列关系式人均资本与产出的关系人均资本与产出的关系式y=ka是在不考虑技术因素A的情况下，由柯布-道格拉斯生产函数Y=AKaL1-a等式两边同时除以L所得出的。从人均资本与产出的关系式中，我们可以考察出资本与产出之间的变化规律。1964年日本经济学家稻田献一总结出这类生产函数的6个满足条件，从而很好的刻画了这一生产函数的特征。稻田条件：1.资本为零时，产出也为零。（即k=0,时y=0）——但现实中资本为零时产出并不一定为零，这个假设条件可以使模型的起始条件从零开始研究；2.资本与产出的关系是连续的；3.资本增加，产出也增长。（即k↑，y↑）4.随着资本的增加，产出的增加量会越来越小，即资本边际收益会递减。5.资本很小时，少量的增加资本，产出就会有很大的提升。（即k→0时，y′→∞）——这解释了为什么贫穷的国家只要获得少量的投资，经济增长就能有很大的提升。6.资本很大时，继续增加资本，产出也不会有很大的提升，最终将达到一个平衡的“稳态”。（即k→∞时，y′→0）——这解释了为什么富裕的国家即便再加大投资，经济也很难有大的增长，例如美国和日本。根据上面的稻田条件，我们可以画出人均资本与产出的关系图。柯布-道格拉斯生产函数Y=AKaL1-a人均资本与人均产出关系式y=ka人均资本形成的关系式△kt=s*yt-δ*kt引入人口增长和技术进步△kt=s*A*yt-(δ+n)*kt经济增长达到稳态的收敛期T/2=-ln(0.5)/(1-a)*(δ+n+g)Y：总产出GDPA:技术因素K:资本存量L：劳动力投入a:资本所占产出的份额0