3-4静定桁架受力分析VIP免费

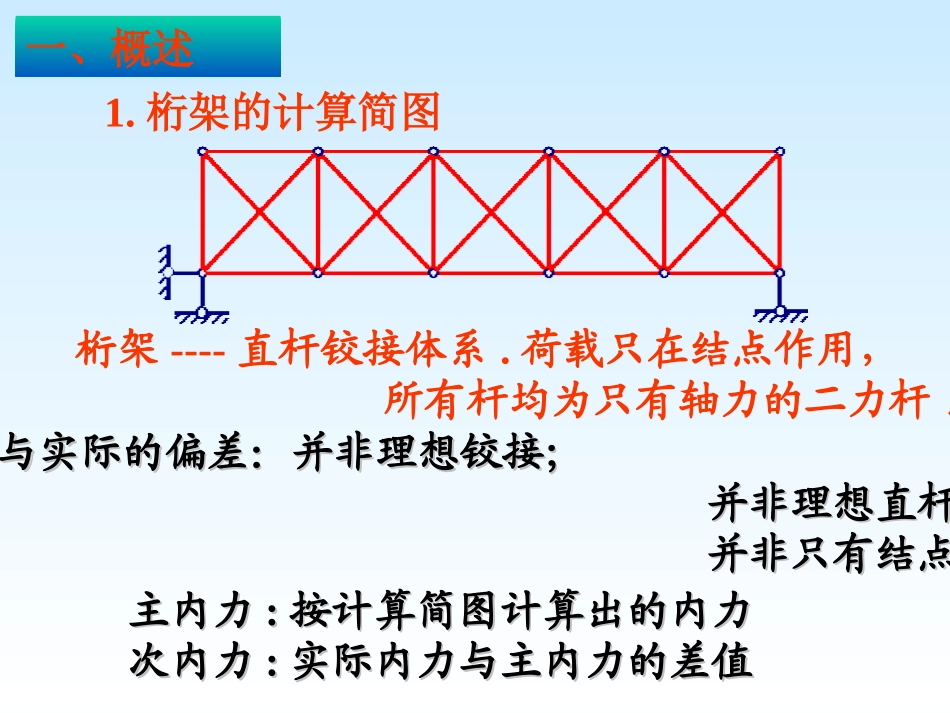
内容提要静定桁架3.4-1基本概念3.4-2.节点法3.4-3.截面法主内力主内力::按计算简图计算出的内力按计算简图计算出的内力次内力次内力::实际内力与主内力的差值实际内力与主内力的差值简图与实际的偏差：并非理想铰接；简图与实际的偏差：并非理想铰接；并非理想直杆；并非理想直杆；并非只有结点荷载并非只有结点荷载；；一、概述桁架----直杆铰接体系.荷载只在结点作用，所有杆均为只有轴力的二力杆..1.桁架的计算简图简支桁架中杆件的名称上弦杆腹杆下弦杆结间：桁架下弦杆相邻结点间的区间。结间长度：桁架下弦杆相邻结点间的水平距离。2.桁架的分类按几何组成分类：简单桁架—在基础或一个铰结三角形上依次加二元体构成的联合桁架—由简单桁架按基本组成规则构成复杂桁架—非上述两种方式组成的静定桁架简单桁架简单桁架联合桁架复杂桁架简支平面桁架按弦杆外形分类a)平行弦桁架b)折线弦桁架c)三角形桁架d)抛物线桁架桁架按维数分类平面桁架平面桁架空间桁架空间桁架简支平面桁架按受力特点分类梁式桁架梁式桁架拱式桁架拱式桁架3.桁架内力的计算方法静定桁架的内力计算基本方法为：结点法截面法注：实际应用一般是这两种基本方法的灵活选择、联合应用。对于简单桁架,若与组成顺序相反依次截取结点,可保证求解过程中一个方程中只含一个未知数.结点单杆:利用结点的一个平衡方程可求出内力的杆件单杆单杆1N2N01N02N零杆：在桁架中，轴力为零的杆件。（1）两根杆的结点（a）若结点上无荷载，则二杆全为零。（a）（b）若荷载沿其中一杆的方向，则该杆轴力为P，另一杆为零杆。1N2NPN102N（b）P（2）有单杆的结点1N2N3N21NNPN3（a）在图示荷载作用下单杆3的轴力利用可求。0Y（b）在荷载沿单杆作用下，则单杆轴力等于P，另两杆轴力相等。（c）单杆结点上无荷载作用，则单杆轴力等于0。（b）1N2N3N21NNsin3PNP（a）α1N2N3N21NN03N（c）P判定图示桁架中的零杆.ABCDEFGHIPP解:AB和BC是零杆.CI是零杆.EG是零杆.EH是零杆.FP/2FP/2FPFPFP例:试指出零杆PP受力分析时可以去掉零杆,是否说该杆在结构中是可有可无的?0000P结点法的计算步骤:1.去掉零杆2.逐个截取具有单杆的结点,由结点平衡方程求轴力.二、结点法取隔离体时,每个隔离体只包含一个结点的方法.隔离体上的力是平面汇交力系,只有两个独立的平衡方程可以利用,故一般应先截取只包含两个未知轴力杆件的结点.2.结点法适用范围简单桁架、在桁架中三根杆件的结点上，如有两根杆在一条直线上，另一根在独立方向上的杆称为“单杆”。结点有单杆的桁架。3.结点法计算时，通常假定未知轴力为拉力。若所的结果为负，则为压力。1.原理2/PPPPPP2/PAFECDBGIJHa6LKa3AYAXBYPYA30AXPYB31.求支座反力例：解题要点：力的投影三角形与杆长的投影三角形相似yxxyNNNlll其它杆件轴力求法类似.求出所有轴力后,应把轴力标在杆件旁.2/PPPPPP2/PAFECDBGIJHa6LKa3AYAXBYPYA30AXPYB31.求支座反力2.取结点ACCENCDNCANAYAACNADN2/PDCNDDENDFNDANP2/25,02/32/2,0PNPPNFADADy2/5,02/2,0PNNNFACACADx3.取结点C2/5,0PNNNCACECD4.取结点DPPNNFDADF222/2,02/2,0PNFDE练习：已知：荷载与尺寸如图；求：每根杆所受力.解：取整体，画受力图.0xF0AxF0BM8581061041020AyF得20AyFkN0yF400AyByFF得20kNByF求各杆内力取节点A00yADxACFFFF取节点C000xCFyCDFFFF取节点D0,0yDFDExFFFF取节点E00yEGxEFFFFF练习：一屋顶桁架的尺寸及荷载如图所示,试用节点法求每根杆件的内力.5kN5kN10kN10kN10kNAHBCDEFG4×4=16m2×3=6m解:取整体为研究对象画受力图.RARH去掉零杆BC和FG5kN5kN10kN10kN10kNAHBCDEFG4×4=16m2×3=6mmA(Fi)=0-10×(4+8+12)-5×16+16RH=0RH=20kNRA=20kN取节点A为研究对象画受力图.5kNA20kNSACSABsin=0.6cos=0.8Yi=020-5+0.6SAC=0SAC=-25kNXi=0(-25)×0.8+SAB=0SAB=20kN取节点B为研究对象画受力...