2.3.4平面与平面垂直的性质定理(典型)VIP免费

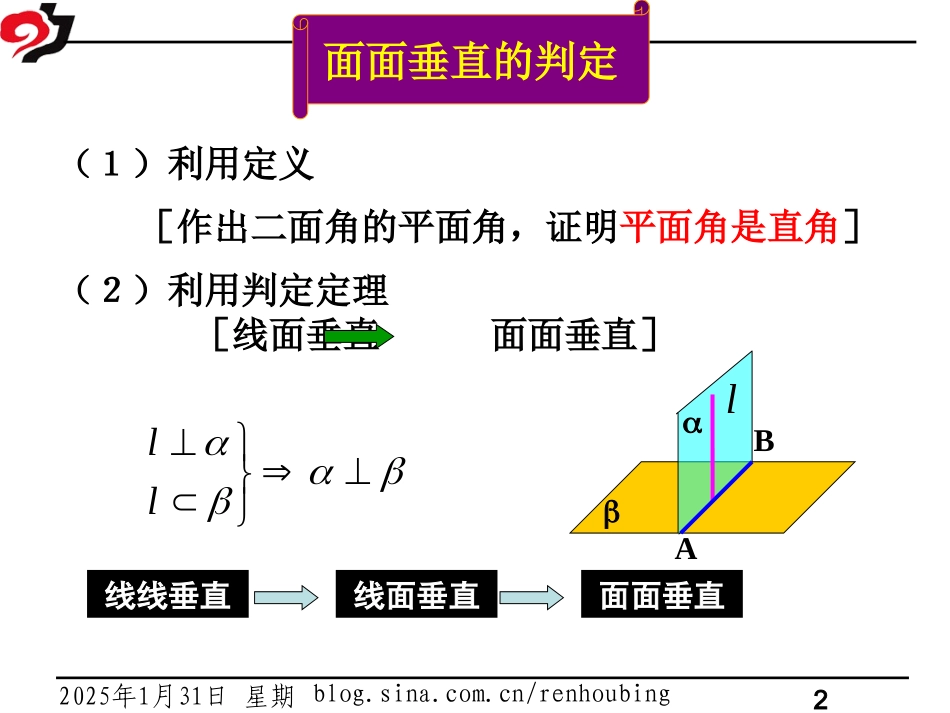
blog.sina.com.cn/renhoubing22025年1月31日星期五（１）利用定义（２）利用判定定理［线面垂直面面垂直］lllAB线面垂直面面垂直线线垂直面面垂直的判定［作出二面角的平面角，证明平面角是直角］blog.sina.com.cn/renhoubing32025年1月31日星期五A1D1B1C1CBADαβEF思考1如图，长方体中，α⊥β,(1)α里的直线都和β垂直吗？(2)什么情况下α里的直线和β垂直？与AD垂直不一定blog.sina.com.cn/renhoubing42025年1月31日星期五思考2垂足为B，那么直线AB与平面β的位置关系如何？,CD，,ABαβABDCE,ABCD垂直blog.sina.com.cn/renhoubing52025年1月31日星期五 ,∴AB⊥BE.又由题意知AB⊥CD,且BECD=B垂足为B.∴AB⊥.则∠ABE就是二面角的平面角.CD证明:在平面内作BE⊥CD,αβABDCEblog.sina.com.cn/renhoubing62025年1月31日星期五平面与平面垂直的性质定理符号表示:CDABABABCDABCDBDCAB两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．面面垂直线面垂直blog.sina.com.cn/renhoubing72025年1月31日星期五思考3设平面⊥平面，点P在平面内，过点P作平面的垂线a，直线a与平面具有什么位置关系?aβαP直线a在平面内blog.sina.com.cn/renhoubing82025年1月31日星期五1aa,aa.例如图，已知平面，，，直线满足，试判断直线与平面的位置关系αβAbal分析：寻找平面α内与a平行的直线.blog.sina.com.cn/renhoubing92025年1月31日星期五解：在α内作垂直于交线的直线b， ∴ ∴ab.∥又 ∴a∥α.即直线a与平面α平行.，b，a，a，结论：垂直于同一平面的直线和平面平行（）.aαβAbal与,aa//，ablog.sina.com.cn/renhoubing102025年1月31日星期五ABAB.aaa已知平面，，直线∥，，变试判断直线与的位置关系式αβAbalB垂直blog.sina.com.cn/renhoubing112025年1月31日星期五abαβlγmn,.ll例2.已知平面，，满足，，求证：blog.sina.com.cn/renhoubing122025年1月31日星期五如果两个相交平面都垂直于另一个平面，那么这两个平面的交线垂直于这个平面.结论αβγl如图：ll，，blog.sina.com.cn/renhoubing132025年1月31日星期五两个平面垂直应用举例例1如图，AB是⊙O的直径，点C是⊙O上的动点，过动点C的直线VC垂直于⊙O所在平面，D、E分别是VA、VC的中点，直线DE与平面VBC有什么关系？试说明理由．平面VAC⊥平面VBC及DEVC⊥．AC垂直于平面VBC及DE∥AC.blog.sina.com.cn/renhoubing142025年1月31日星期五例2．S为三角形ABC所在平面外一点，SA⊥平面ABC，平面SAB⊥平面SBC.求证：AB⊥BC.SCBAD证明：过A点作ADSB⊥于D点. 平面SAB⊥平面SBC,∴AD⊥平面SBC，∴ADBC⊥.又 SA⊥平面ABC，∴SABC⊥.AD∩SA=A∴BC⊥平面SAB.∴BCAB.⊥blog.sina.com.cn/renhoubing152025年1月31日星期五练习：1.如图，以正方形ABCD的对角线AC为折痕，使△ADC和△ABC折成相垂直的两个面，求BD与平面ABC所成的角。ABCDDABCOO折成blog.sina.com.cn/renhoubing162025年1月31日星期五2.如图，平面AED⊥平面ABCD，△AED是等边三角形，四边形ABCD是矩形，（1）求证：EACD⊥MDECAB（2）若AD＝1，AB＝，求EC与平面ABCD所成的角。2blog.sina.com.cn/renhoubing172025年1月31日星期五(2012·北京模拟)如图，正方形ADEF与梯形ABCD所在的平面互相垂直，AD⊥CD，AB∥CD，AB=AD=2，CD=4，M为CE的中点.(1)求证：BM∥平面ADEF；(2)求证：平面BDE⊥平面BEC.blog.sina.com.cn/renhoubing182025年1月31日星期五【证明】(1)取DE中点N，连接MN，AN.在△EDC中，M，N分别为EC，ED的中点，所以MN∥CD，且MN=CD.由已知AB∥CD，AB=CD，所以MN∥AB,且MN=AB,所以四边形ABMN为平行四边形.所以BM∥AN.又因为AN平面ADEF，且BM平面ADEF，所以BM∥平面ADEF.1212blog.sina.com.cn/renhoubing192025年1月31日星期五(2)因为四边形ADEF为正方形，所以ED⊥A...