4.1平面向量的加法减法运算VIP免费

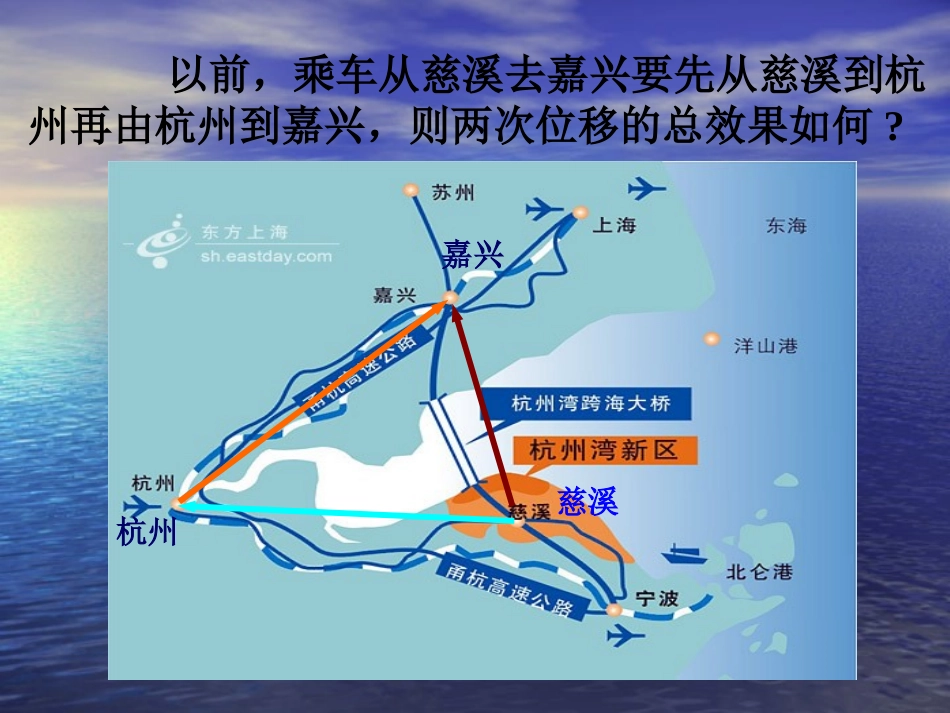
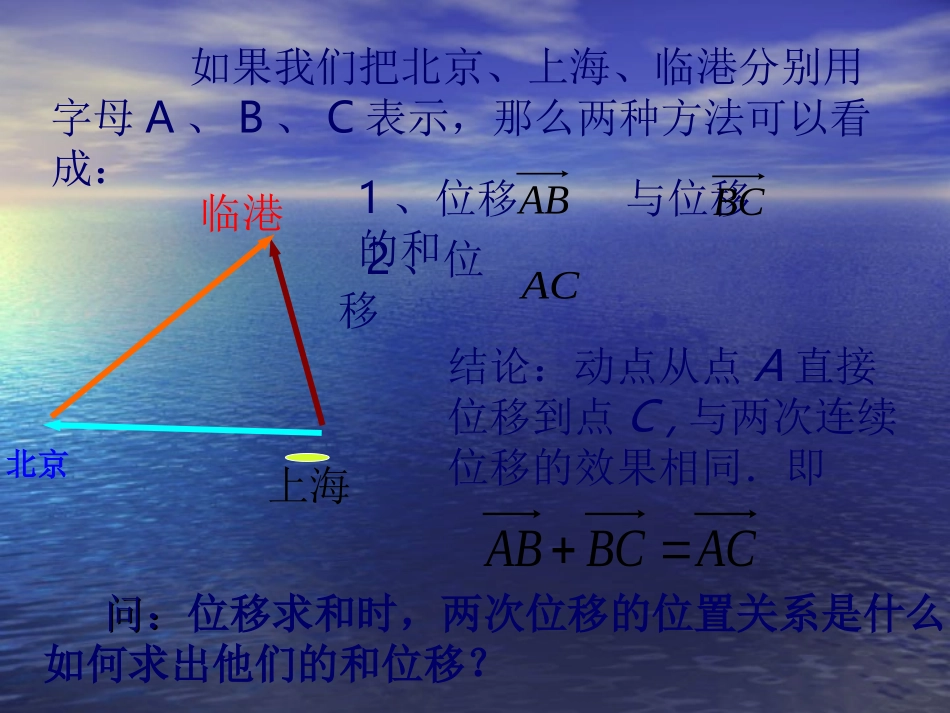
§2.2.1§2.2.1向量加法运算向量加法运算及其几何意义及其几何意义§4.1§4.1平面向量的加法运算平面向量的加法运算以前，乘车从慈溪去嘉兴要先从慈溪到杭州再由杭州到嘉兴，则两次位移的总效果如何?嘉兴慈溪杭州1、位移与位移的和ABBC2、位移AC�结论：动点从点A直接位移到点C,与两次连续位移的效果相同．即ACBCAB如果我们把北京、上海、临港分别用字母A、B、C表示，那么两种方法可以看成：问：问：位移求和时，两次位移的位置关系是什么？如何求出他们的和位移？上海临港北京BCAA定义：求两个向量和的运算,叫做向量的加法.向量的加法a+b=AB+BC=AC注意：两个向量的和仍然是一个向量两个向量的和仍然是一个向量作平移,首尾相连,由起点指向终点.A1在平面内任取一点作法：bBC,aAB2作baAC3则向量aba+b首尾相连ab向量加法的三角形法则abc练习：已知向量，求作向量,abab首尾相连bac例1：在平行四边形ABCD中，求作＋ABAD我们先来找一找在这个平行四边形中相等的向量：DCABBCADCDBACBDA解：因为，所以．BCADACBCABADAB例1：在平行四边形ABCD中，1.说一说两个相加向量的位置特点；ACADAB2.两个向量相加的和向量与这两个向量的位置关系；例1：在平行四边形ABCD中，ACADAB这种求不共线的两个向量和的方法叫做的和正好是以向量、为邻边的平行四边形的对角线AC表示的向量．ABADADAB向量加法的平行四边形法则首首相连作平移,共起点,四边形,对角线BabCDAA作法:(1)在平面内任取一点AbADaAB,(2)作baAC则(3)以AB,AD为邻边作平行四边形ABCD向量的加法首首相连已知向量a,b,用向量加法的平行四边形法则求作向量a+b.练一练如图,已知用向量加法的平行四边形法则作出baba,（1）abbbaababa（2）首首相连回顾例1：平行四边形ABCD中，ACADAB解：因为，DCABACDCADABAD所以ABADADAB即bAD,aAB令于是abba这就是向量的加法交换律.(与数量的加法交换律相似)问:能否不移动向量,而移动向量？结果是否和原来一样呢？ADABDDAABBCC例2．如图所示是平行四边形ABCD，化简下列各式：BCAB)1(ADAB)2(CDAD)3(解解：：ACBCAB)1(ACADAB)2(BDCDAD即(3)因为，BCADBDCDBCCDAD所以abba热身运动：拔河热身运动：拔河1、相反向量：与非零向量长度相等，且方向相反的向量叫做向量的相反向量，记作。aaa说明：①规定00②性质aaaaaa02、向量的减法：向量a与向量b的负向量的和定义为向量a与向量b的差，即baba求两个向量差的运算叫作向量的减法1、向量减法法则：已知向量，不共线，求作向量，使abcbacab作法：在平面内任取一点O，作，，则aOAbOBOBOAOBOABOOAOABOBAOBAabbaaaabbbb向量减法法则BAOBOAOBAabba归纳概括：同起点，连终点，指向被减⑵连接两向量的终点,⑶方向指向被减向量⑴将两向量移到共同起点2、小试牛刀已知向量和（如下图），请分别画出和abbaababab①共线同向②共线反向aABCabaABC3、动脑思考若、共线时，怎样作？baabbbaaabbbCBACABbaaaaabbbCBACABbaab例1已知如图所示向量、，请画出向量abbabaOabABba例2化简：⑴OAOD⑵DCBDACAB解：⑴OAODAD⑵DCBDACABDCBDCBDCCDCC01、已知、，求作abbaaaaabbbb2、快速抢答：______ADAB______BCBA_____OBOA_____MPMNQPNQ_____DBADBCAB_____GEMGANAM_____DPMPMNMD______BDACCDAB_____DADCBCAB_____DCBDACAB_____DBOCOB_____COBOOCOADBCABA0BCNECDBA00MN0备选题：如图所示，在平行四边形ABCD中，设，，试用，表示向量、、。aABbADabACBDDBABCDab1、向量减法的定义及其几何意义2、正确熟练地掌握向量减法法则：共起点、连终点、指向被减作业：作业：•教材教材P89P89，课堂练习第，课堂练习第11、、22题题