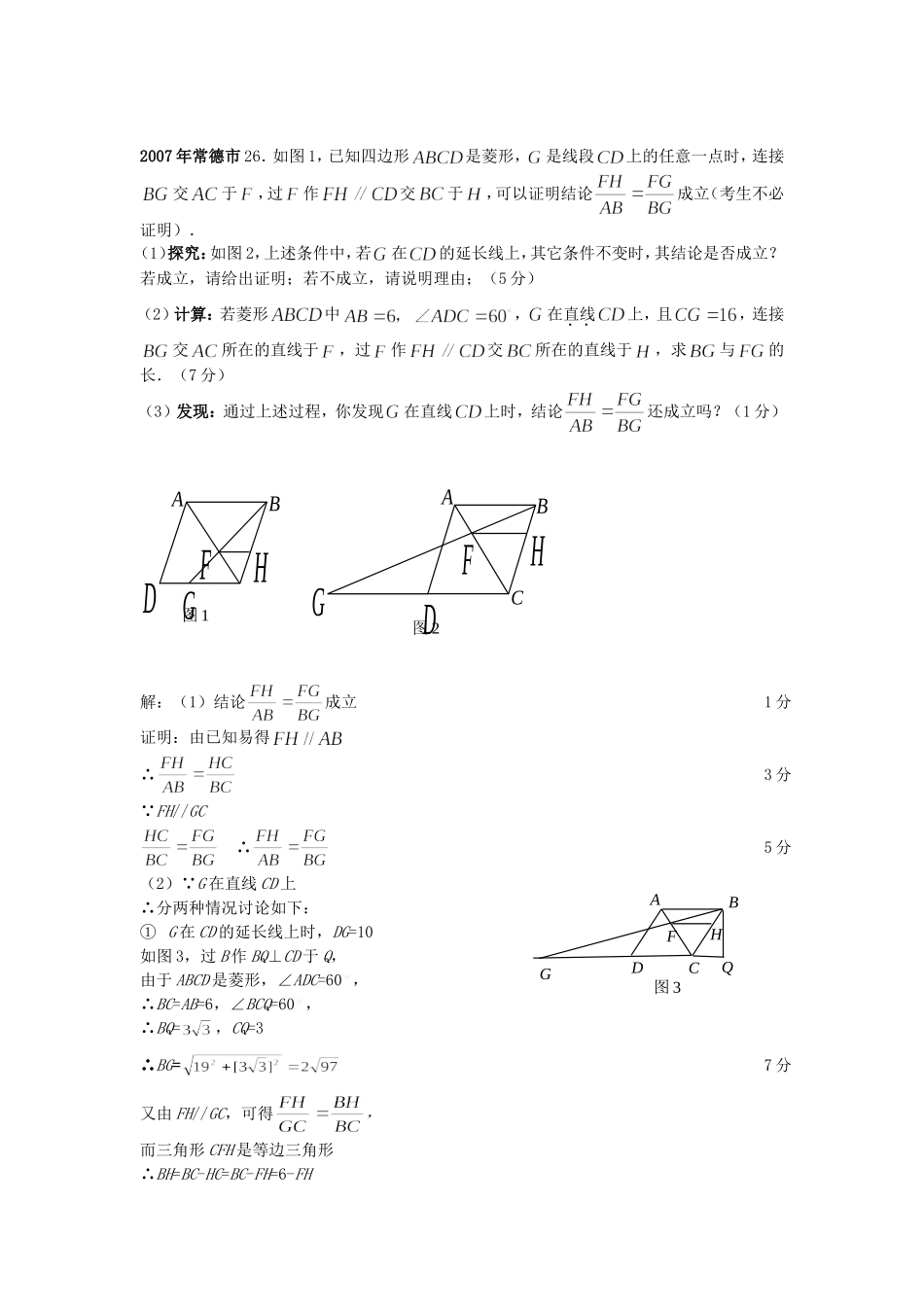
2007年常德市26.如图1,已知四边形是菱形,是线段上的任意一点时,连接交于,过作交于,可以证明结论成立(考生不必证明).(1)探究:如图2,上述条件中,若在的延长线上,其它条件不变时,其结论是否成立?若成立,请给出证明;若不成立,请说明理由;(5分)(2)计算:若菱形中,在直线上,且,连接交所在的直线于,过作交所在的直线于,求与的长.(7分)(3)发现:通过上述过程,你发现在直线上时,结论还成立吗?(1分)解:(1)结论成立1分证明:由已知易得∴3分 FH//GC∴5分(2) G在直线CD上∴分两种情况讨论如下:①G在CD的延长线上时,DG=10如图3,过B作BQ⊥CD于Q,由于ABCD是菱形,∠ADC=60,∴BC=AB=6,∠BCQ=60,∴BQ=,CQ=3∴BG=7分又由FH//GC,可得而三角形CFH是等边三角形∴BH=BC-HC=BC-FH=6-FH图1ABDFHG图2ABCDFHGBADC图3FHGQ∴,∴FH=由(1)知∴FG=9分②G在DC的延长线上时,CG=16如图4,过B作BQ⊥CG于Q,由于ABCD是菱形,∠ADC=600,∴BC=AB=6,∠BCQ=600,∴BQ=,CQ=3∴BG==14………………………………11分又由FH//CG,可得∴,而BH=HC-BC=FH-BC=FH-6∴FH=又由FH//CG,可得∴BF=∴FG=14+12分(3)由(2)可知:当G在CD的延长线上时,,所以成立;当G在DC的延长线上时,,所以成立结合上述过程,发现G在直线CD上时,结论还成立.13分德州市二〇〇七年23.(本题满分10分)已知:如图14,在中,为边上一点,ABCFHGD图4CADB图14,,.(1)试说明:和都是等腰三角形;(2)若,求的值;(3)请你构造一个等腰梯形,使得该梯形连同它的两条对角线得到8个等腰三角形.(标明各角的度数)解:(1)在中,,.…………1分在与中,;,.…………2分.和都是等腰三角形.4分(2)设,则,即.……6分解得(负根舍去).…………8分(3)如右图所示:等腰梯形ABCD中,AD=DC=CB,两条对角线AC和BD相交于O点,该梯形连同它的两条对角线可得到8个等腰三角形:2007年福建省宁德市26.(本题满分14分)已知:矩形纸片中,厘米,厘米,点在上,且厘米,点是边上一动点.按如下操作:步骤一,折叠纸片,使点与点重合,展开纸片得折痕(如图1所示);3636363636367272108(有8个等腰三角形)步骤二,过点作,交所在的直线于点,连接(如图2所示)(1)无论点在边上任何位置,都有=(填“”、“”、“”号);(2)如图3所示,将纸片放在直角坐标系中,按上述步骤一、二进行操作:①当点在点时,与交于点点的坐标是(0,3);②当厘米时,与交于点点的坐标是(6,6);③当厘米时,在图3中画出(不要求写画法),并求出与的交点的坐标;(3)点在运动过程,与形成一系列的交点观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式.解:③画图,如图所示,设与交于点.在中,,.,,.又,....(3)这些点形成的图象是一段抛物线.函数关系式:.2007年福建省三明市26.(本小题满分12分)如图①,②,在平面直角坐标系中,点的坐标为(4,0),以点为圆心,4为半径的圆APBCMD(P)EBC图10(A)BCDE6121824xy612181Q2Q图3ANPBCMDEQT图20(A)BCDE6121824xy612181Q2Q3QFMGP与轴交于,两点,为弦,,是轴上的一动点,连结.(1)求的度数;(2分).(2)如图①,当与相切时,求的长;(3分)(3)如图②,当点在直径上时,的延长线与相交于点,问为何值时,是等腰三角形?(7分)解:(2) CP与相切,∴.∴.又 (4,0),∴.∴.∴.5分(3)①过点作,垂足为,延长交于, 是半径,∴,∴,∴是等腰三角形.又 是等边三角形,∴=2.②解:过作,垂足为,延长交于,与轴交于, 是圆心,∴是的垂直平分线.∴.∴是等腰三角形,作轴于,在中, ,∴.∴点的坐标(4+,).在中, ,∴.∴点坐标(2,).设直线的关系式为:,则有解得:∴.当时,.∴.贵阳市2007年25.(本题满分12分)如图14,从一个直径是2的圆形铁皮中剪下一个圆心角为的扇形.(1)求这个扇形的面积(结果保留).(3分)(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.(4分)(3)当的半径为任意...