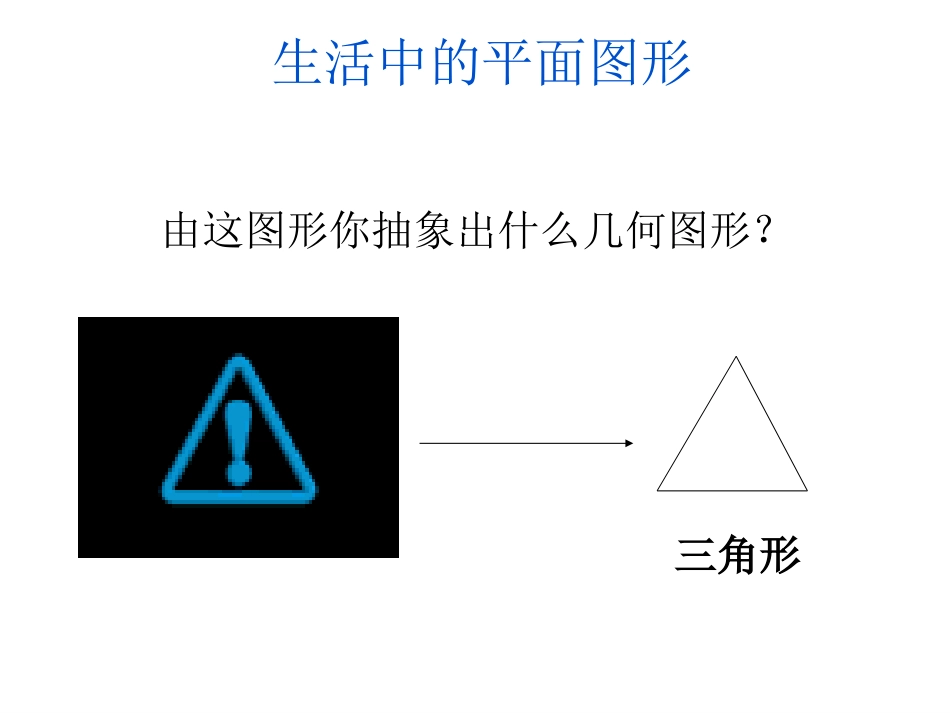
11.3.111.3.1多边形及多边形及多边形的内角和多边形的内角和生活中的平面图形由这图形你抽象出什么几何图形?三角形长方形生活中的平面图形由这图形你抽象出什么几何图形?由这图形你抽象出什么几何图形?四边形生活中的平面图形六边形生活中的平面图形由这图形你抽象出什么几何图形?八边形生活中的平面图形由这图形你抽象出什么几何图形?你能仿照三角形的定义给出多边形的定义吗?不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形三角形长方形六边形四边形八边形在平面内,由若干条不在同一条直线上的线段首尾顺次相接组成的图形叫做多边形。多边形的定义ADCEB内角外角n边形有______个顶点,_______条边个内角,_______个外角n2nnn多边形的有关概念比一比你能说出这两幅图形的异同点吗?(1)(2)如图(1)这样,画出多边形的任何一条边所在的直线,整个多边形都在这条直线的同一侧,那么这个多边形就是凸多边形。如果没有特殊指明,初中阶段所说的多边形都是凸多边形.问:下列哪个是凸多边形?想一想:在平面内,内角都相等,边也都相等的多边形叫做正多边形等边三角形正方形正五边形正六边形问题:缺少以上其中一个条件还是不是正多边形?请举出反例ADCEB连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。还有过点A的对角线吗?请观察思考,如何添加辅助线将多边形划分为多个三角形?我们不能用度量或剪拼的方法一一验证所有多边形的内角和。辅助线多边形内角和三角形内角和转化未知已知探索边数n从一个顶点出发的对角线的条数从一个顶点出发的对角线分成的三角形个数总的对角线条数n边形内角和n-3n-2n(n-3)2(n-2)x180°……ADBC1.过多边形一个顶点引出对角线,把多边形分成若干个三角形,把多边形内角和转化为求各三角形内角和。ABCD2.在多边形内任取一点,连接该点与各顶点,得到若干个三角形,把多边形内角和转化为三角形内角和的问题。3.在多边形边上任取一点,连接该点与其不相邻的各顶点,得到若干个三角形,把多边形内角和转化为三角形内角和问题。ADBCEn边形内角和=(n-2)x180°……ABCD例1:如果一个四边形的一组对角互补,那么另一组对角有什么关系?如果四边形的一组对角互补,那么另一组对角也互补。练习11、求八边形的内角和的度、求八边形的内角和的度数数..那七边形的度数又为多少那七边形的度数又为多少呢?呢?解:(解:(8-28-2))×180°=1080°×180°=1080°((7-27-2))×180°=900°×180°=900°答:八边形的内角和是答:八边形的内角和是1080°.1080°.七边形的内角和是七边形的内角和是900°.900°.2、过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形.这个多边形是______边形。七3、(1)如果一个多边形从一个顶点出发可作14条对角线,那么这个多边形是_____边形。(2)如果一个多边形共有14条对角线,那么这个多边形是____边形。十七七4、已知一个多边形的内角和等于1440°,求它的边数。解:设这个多边形的边数为n,根据题意可得:(n-2)×180°=1440°解得:n=10答:这个多边形是十边形。5、已知多边形的每一内角为150°,求这个多边形的边数.解:设这个多边形的边数为n,根据题意,得(n-2)×180=150n解这个方程,得n=12经检验,符合题意答:这个多边形的边数为12.6、一个多边形只截去一个角(截线不经过顶点),形成另一个多边形的内角和为2520°,则原多边形的边数为多少?7、小明在计算某个多边形的内角和时,由于粗心他漏掉一个内角,求得的内角和1680°,你能否求得正确结果呢?8、如图,直线a∥b,那么∠1+∠2+∠3=。ab123